Consider a radioactive nucleus A which decays to a stable nucleus C through the following sequence
A→B→C
Here B is an intermediate nuclei which is also radioactive. Considering that there are N0 atoms of A initially , plot the praph showing the variation of number of atoms of A and B versus time.
To solve the problem of plotting the variation of the number of atoms of radioactive nuclei A and B versus time, we can follow these steps:
Step 1: Understand the Decay Process
- Nucleus A decays into nucleus B, which is also radioactive, and then B decays into stable nucleus C.
- Initially, we have N0 atoms of A, and the number of atoms of B and C is zero.
Step 2: Write the Decay Equations
- The decay of A can be described by the equation:
NA(t)=N0e−λAt
where λA is the decay constant for A.
- The number of atoms of B at any time t can be derived from the decay of A and the decay of B:
NB(t)=λA∫t0NA(t′)e−λB(t−t′)dt′
where λB is the decay constant for B.
Step 3: Simplify the Equation for B
- Since NA(t)=N0e−λAt, we can substitute this into the equation for NB(t):
NB(t)=λAN0∫t0e−λAt′e−λB(t−t′)dt′
This integral can be solved to give:
NB(t)=λAN0λB−λA(e−λAt−e−λBt)
for λB≠λA.
Step 4: Plot the Graphs
- Graph for N_A vs. Time (t):
- The graph of NA(t) is an exponential decay curve starting from N0 and approaching zero as time increases.
- Graph for N_B vs. Time (t):
- The graph of NB(t) will initially increase as A decays into B, reaching a maximum point, and then will decrease as B decays into C.
Step 5: Combine the Graphs
- On a single graph, plot both NA(t) and NB(t) against time.
- NA(t) will show a continuous decline, while NB(t) will show an initial rise to a peak followed by a decline.
Final Graph
- The final graph will have two curves:
- One curve representing NA(t) which decreases exponentially.
- Another curve representing NB(t) which increases to a maximum and then decreases.
- Nucleus A decays into nucleus B, which is also radioactive, and then B decays into stable nucleus C.
- Initially, we have N0 atoms of A, and the number of atoms of B and C is zero.
- The decay of A can be described by the equation:
NA(t)=N0e−λAt
where λA is the decay constant for A.
- The number of atoms of B at any time t can be derived from the decay of A and the decay of B:
NB(t)=λA∫t0NA(t′)e−λB(t−t′)dt′
where λB is the decay constant for B.
- Since NA(t)=N0e−λAt, we can substitute this into the equation for NB(t):
NB(t)=λAN0∫t0e−λAt′e−λB(t−t′)dt′
This integral can be solved to give:
NB(t)=λAN0λB−λA(e−λAt−e−λBt)
for λB≠λA.
- Graph for N_A vs. Time (t):
- The graph of NA(t) is an exponential decay curve starting from N0 and approaching zero as time increases.
- The graph of NB(t) will initially increase as A decays into B, reaching a maximum point, and then will decrease as B decays into C.
- On a single graph, plot both NA(t) and NB(t) against time.
- NA(t) will show a continuous decline, while NB(t) will show an initial rise to a peak followed by a decline.
- The final graph will have two curves:
- One curve representing NA(t) which decreases exponentially.
- Another curve representing NB(t) which increases to a maximum and then decreases.
Topper's Solved these Questions
Similar Questions
A radioactive nucleus A with a half life T, decays into nucleus B. At t=0, there is no nucleus B. At some time t, the ratio of the number of B to that of A is 0.3 . Then, t is given by
View SolutionRadioactive nucleus A decays into B with half-life 10sec. A also convert into C with half-life 100sec. Find half-life of A for both emission.
View SolutionThe variation of decay rate of two radioactive samples A and B with time is shown in fig.
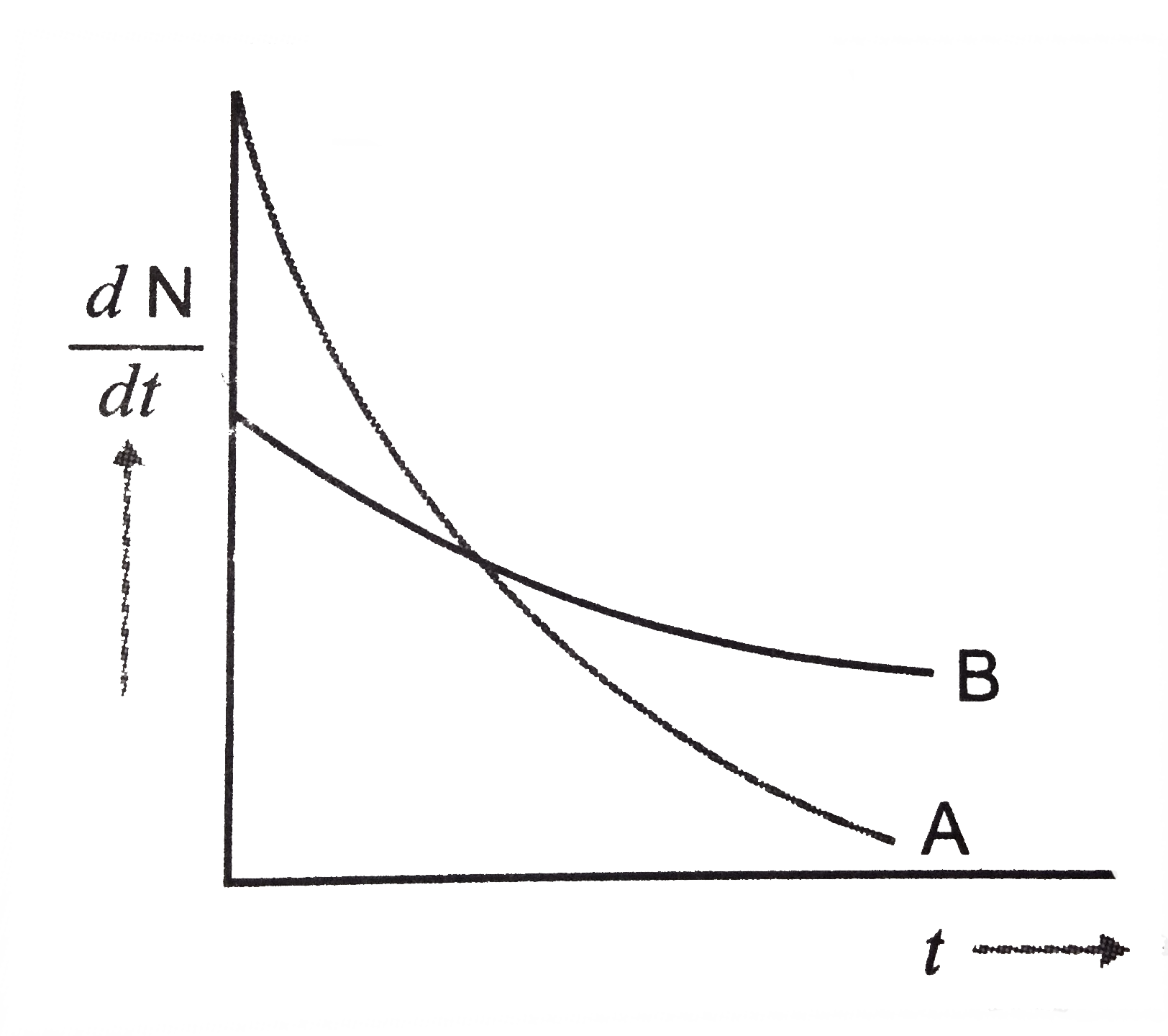
Which of the following statements are true?View SolutionThe variation of decay rate of two radioactive samples A and B with time is shown in fig.

Which of the following statements are true?View SolutionA factory produces a radioactive substance A at a constant rate R which decays with a decay constant λ to form a stable substance. Find (a) the number of nuclei of A and (b) number of nuclei of B, at any time t assuming the production of A starts at t=0. (c ) Also, find out the maximum number of nuclei of A present at any time during its formation.
View SolutionNuceli A and B convert into a stable nucleus C. Nucleus A is converted into C by emitting 2αparticels and 3β-particles. Nucleus B is converted into C by emitting one α-particle and 5β-particles. At time t=0, nuclei of A are 4N0 and nuceli of B are N0. Initially, number of nuclei of C are zero. Half-life of A (into conservation of C) is 1min and that of B is 2min. Find the time (in minutes) at which rate of disintegration of A and B are equal.
View SolutionA and B are isotopes. B and C are isobars. All three are radioactive. Which one of the following is true.
View SolutionA parent radioactive nucleus A (decay constant λA) converts into a radio-active nucleus B of decay constant λb, initially, number of atoms of B is zero At any time Na,Nb are number of atoms of nuclei A and B respectively then maximum velue of Nb.
View SolutionIn a radioactive decay, an emitted electron comes from
(a) the nucleus of atom
(b) the orbit with principal quantum number 1
(c) the inner orbital of the atom
(d) the outermost orbit of the atomView SolutionHeavy radioactive nucleus decay through α−decay also. Consider a radioactive nucleus x. It spontaneously undergoes decay at rest resulting in the formation of a daughter nucleus y and the emission of an α− particle. The radioactive reaction can be given by
x→y+α
However , the nucleus y and the α− particle will be in motion. Then a natural question arises that what provides kinetic energy to the radioactive products. In fact, the difference of masses of the decaying nucleus and the decay products provides for the energy that is shared by the daughter nucleus and the α− particle as kinetic energy . We know that Einstein's mass-energy equivalence relation E=mc2. Let mx,my and mα be the masses of the parent nucleus x, the daughter nucleus y and α− particle respectively. Also the kinetic energy of α− particle just after the decay is E0. Assuming all motion of to be non-relativistic.
Which of the following is correct ?View Solution

