Three copper blocks of masses M1,M2andM3 kg respectively are brought into thermal contact till they each equilibrium. Before contact, they were at T1,T2,T3(T1>T2>T3). Assuming there is no heat loss to the surroundings, the equilibrium temperature T is (s is specific heat of copper)
T=T1+T2+T33
T=M1T1+M2T2+M3T3M1+M2+M3
T=M1T1+M2T2+M3T33(M1+M2+M3)
T=M1T1s+M2T2s+M3T3sM1+M2+M3
The correct Answer is:B
To find the equilibrium temperature T of the three copper blocks, we can follow these steps:
Step 1: Understand the Heat Transfer
When the three copper blocks are brought into thermal contact, heat will flow from the hotter blocks to the cooler blocks until they reach thermal equilibrium. Since there is no heat loss to the surroundings, the heat lost by the hotter blocks will equal the heat gained by the cooler blocks.
Step 2: Set Up the Heat Transfer Equation
Let:
- M1 be the mass of the first block, initially at temperature T1
- M2 be the mass of the second block, initially at temperature T2
- M3 be the mass of the third block, initially at temperature T3
Given that T1>T2>T3, we can express the heat lost and gained as follows:
- Heat lost by block 1: Q1=M1s(T1−T)
- Heat lost by block 2: Q2=M2s(T2−T)
- Heat gained by block 3: Q3=M3s(T−T3)
Step 3: Apply the Conservation of Energy
According to the principle of conservation of energy, the total heat lost by blocks 1 and 2 should equal the total heat gained by block 3:
Q1+Q2=Q3
Substituting the expressions for heat:
M1s(T1−T)+M2s(T2−T)=M3s(T−T3)
Step 4: Simplify the Equation
Since s (specific heat) is a common factor, we can cancel it out from the equation:
M1(T1−T)+M2(T2−T)=M3(T−T3)
Expanding this gives:
M1T1−M1T+M2T2−M2T=M3T−M3T3
Step 5: Rearrange the Equation
Rearranging the terms to isolate T:
M1T1+M2T2+M3T3=M1T+M2T+M3T
Combining the terms involving T:
M1T1+M2T2+M3T3=(M1+M2+M3)T
Step 6: Solve for the Equilibrium Temperature T
Now, we can solve for T:
T=M1T1+M2T2+M3T3M1+M2+M3
This gives us the equilibrium temperature of the three blocks.
Final Answer
The equilibrium temperature T is:
T=M1T1+M2T2+M3T3M1+M2+M3
When the three copper blocks are brought into thermal contact, heat will flow from the hotter blocks to the cooler blocks until they reach thermal equilibrium. Since there is no heat loss to the surroundings, the heat lost by the hotter blocks will equal the heat gained by the cooler blocks.
Let:
- M1 be the mass of the first block, initially at temperature T1
- M2 be the mass of the second block, initially at temperature T2
- M3 be the mass of the third block, initially at temperature T3
- Heat lost by block 2: Q2=M2s(T2−T)
- Heat gained by block 3: Q3=M3s(T−T3)
According to the principle of conservation of energy, the total heat lost by blocks 1 and 2 should equal the total heat gained by block 3:
Since s (specific heat) is a common factor, we can cancel it out from the equation:
Rearranging the terms to isolate T:
Now, we can solve for T:
The equilibrium temperature T is:
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - THERMODYNAMICS EXERCISE - MULTIPLE CHOICE QUESTIONS (MORE THAN ONE OPTIONS)5videos
THERMODYNAMICS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - THERMODYNAMICS EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS5videos
THERMODYNAMICS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Very short Answer type Questions15videos
THERMAL PROPERTIES OF MATTER
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - UNITS AND MEASUREMENTS EXERCISE - Long Answer Type Questions9videos
UNITS AND MEASUREMENTS
Similar Questions
Three block of masses m1,m2 and m3 kg are placed in contact with each other on a frictionless table. A force F is applied on the heaviest mass m1, the acceleration of m2 will be
 View Solution
View SolutionThree rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
For a given exothermic reaction ,KPandKp' are the equilibrium constant at temperature T1andT2 respectively .Assuming that heat of reaction is constant in temperature range between T1andT2 , it is readly observed that
AKp>KpBKp<KpCKp=KpDKp=1Kp'
Three blocks of masses m1,m2and m3 are connected by massless strings as shown on a frictionless table. They are pulled with a force T3=40N. If m1=10kg,m2=6kg and m3=4kg the tension T2 will be
 View Solution
View SolutionTwo bodies of different temperatures T1andT2 if brought in thermal contact, do not necessarily settle to the mean temperature (T1+T2)/2. Why?
View SolutionFour thin identical rods AB,AC,BD and EF made of the same material are joined as shown. The free-ends C,D and F are maintained at temperature T1,T2 and T3 respectively. Assuming that there is no loss of heat of the surroundings, the temperature at joint E when the steady state is attained is 1K(2T1+2T2+3T3). Find K(E is mid point of AB)
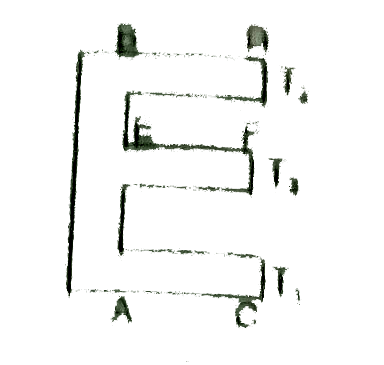 View Solution
View SolutionIf K1 is the equilibrium constant at temperature T1andK2 is the equilibrium constant at temperature T2and If T2>T1 and reaction is endothermic then
View SolutionThe effect of temperature on equilibrium constant is expressed as(T2>T1)
logK2/K1=−ΔH2.303[1T2−1T1]. For endothermic, false statement isView SolutionTwo bolcks to the same metal having same mass and at temperature T1 and T2 respectively ,are brought in contact with each other and allowed to attain thermal equilibrium at constant pressure .The change in entropy ,ΔS for this process is :
View SolutionTwo bolcks to the same metal having same mass and at temperature T1 and T2 respectively ,are brought in contact with each other and allowed to attain thermal equilibrium at constant pressure .The change in entropy ,ΔS for this process is :
View Solution

