Two bodies of different temperatures T1andT2 if brought in thermal contact, do not necessarily settle to the mean temperature (T1+T2)/2. Why?
To understand why two bodies of different temperatures T1 and T2 do not necessarily settle to the mean temperature T1+T22 when brought into thermal contact, we can analyze the situation using the principles of calorimetry. Here’s a step-by-step solution:
Step 1: Define the System
We have two bodies:
- Body 1 with temperature T1, mass m1, and specific heat capacity C1.
- Body 2 with temperature T2, mass m2, and specific heat capacity C2.
Step 2: Establish Heat Transfer
When these two bodies are brought into thermal contact, heat will flow from the hotter body (Body 1, if T1>T2) to the cooler body (Body 2). The heat lost by Body 1 will be equal to the heat gained by Body 2.
Step 3: Write the Heat Transfer Equations
Using the principle of calorimetry, we can express the heat lost and gained as follows:
- Heat lost by Body 1:
Qlost=m1C1(T1−T)
- Heat gained by Body 2:
Qgained=m2C2(T−T2)
Step 4: Set Up the Equation
According to the conservation of energy:
Qlost=Qgained
This gives us the equation:
m1C1(T1−T)=m2C2(T−T2)
Step 5: Rearranging the Equation
Rearranging the equation gives:
m1C1T1−m1C1T=m2C2T−m2C2T2
Bringing all terms involving T to one side:
m1C1T+m2C2T=m1C1T1+m2C2T2
Step 6: Factor Out T
Factoring out T from the left side:
T(m1C1+m2C2)=m1C1T1+m2C2T2
Step 7: Solve for T
Now, solving for T:
T=m1C1T1+m2C2T2m1C1+m2C2
Step 8: Conclusion
This expression shows that the final temperature T is a weighted average of the initial temperatures T1 and T2, weighted by the product of mass and specific heat capacity of each body. Thus, T is not necessarily equal to T1+T22 unless m1C1=m2C2.
Summary
The final temperature depends on the masses and specific heat capacities of the bodies involved, which is why they do not necessarily settle to the mean temperature T1+T22.
---
We have two bodies:
- Body 1 with temperature T1, mass m1, and specific heat capacity C1.
- Body 2 with temperature T2, mass m2, and specific heat capacity C2.
When these two bodies are brought into thermal contact, heat will flow from the hotter body (Body 1, if T1>T2) to the cooler body (Body 2). The heat lost by Body 1 will be equal to the heat gained by Body 2.
Using the principle of calorimetry, we can express the heat lost and gained as follows:
- Heat lost by Body 1:
Qlost=m1C1(T1−T)
- Heat gained by Body 2:
Qgained=m2C2(T−T2)
According to the conservation of energy:
Qlost=Qgained
This gives us the equation:
m1C1(T1−T)=m2C2(T−T2)
Rearranging the equation gives:
m1C1T1−m1C1T=m2C2T−m2C2T2
Bringing all terms involving T to one side:
m1C1T+m2C2T=m1C1T1+m2C2T2
Factoring out T from the left side:
T(m1C1+m2C2)=m1C1T1+m2C2T2
Now, solving for T:
T=m1C1T1+m2C2T2m1C1+m2C2
This expression shows that the final temperature T is a weighted average of the initial temperatures T1 and T2, weighted by the product of mass and specific heat capacity of each body. Thus, T is not necessarily equal to T1+T22 unless m1C1=m2C2.
The final temperature depends on the masses and specific heat capacities of the bodies involved, which is why they do not necessarily settle to the mean temperature T1+T22.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - THERMAL CONDUCTIONEXERCISE - SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM RATE OF HEAT FLOW6videos
THERMAL CONDUCTION
- BOOK - ICSECHAPTER - THERMAL CONDUCTIONEXERCISE - SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM MASS OF ICE MELTED17videos
THERMAL CONDUCTION
- BOOK - ICSECHAPTER - THERMAL CONDUCTIONEXERCISE - SHORT ANSWER QUESTIONS19videos
THERMAL CONDUCTION
- BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 5EXERCISE - Section-D6videos
SELF ASSESSMENT PAPER 5
- BOOK - ICSECHAPTER - THERMAL RADIATION EXERCISE - SELECTED PROBLEMS (from WIEN.S DISPLACEMENT LAW)14videos
THERMAL RADIATION
Similar Questions
A rod of length l with thermally insulated lateral surface consists of material whose heat conductivity coefficient varies with temperature as k=a/T, where a is a constant. The ends of the rod are kept at temperatures T1andT2. Find the function T(x), where x is the distance from the end whose temperature is T1.
View SolutionAssertion : Current versus potential difference (i-V) graph for a conductor at two different temperatures T1 and T2 is shown in figure. Hence T1>T2.

Reason : Resistance of a conductor increases with rise in temperature.View SolutionTwo ideal Carnot engines operate in cascade (all heat given up by one engine is used by the other engine to produce work) between temperatures, T1andT2. The temperature of the hot reservoir of the first engine is T1 and the temperature of the cold reservoir of the second engine is T2. T is temperature of the sink of first engine which is also the source for the second engine. How is T related to T1andT2, if both the engines perform equal amount of work?
View SolutionTwo bolcks to the same metal having same mass and at temperature T1 and T2 respectively ,are brought in contact with each other and allowed to attain thermal equilibrium at constant pressure .The change in entropy ,ΔS for this process is :
View SolutionTwo bolcks to the same metal having same mass and at temperature T1 and T2 respectively ,are brought in contact with each other and allowed to attain thermal equilibrium at constant pressure .The change in entropy ,ΔS for this process is :
View SolutionThe current voltage graphs for a given metalic wire two different temperature T1 and T2 are shown in figure The temperature T2 is greater than T1. Is this statement true or false?
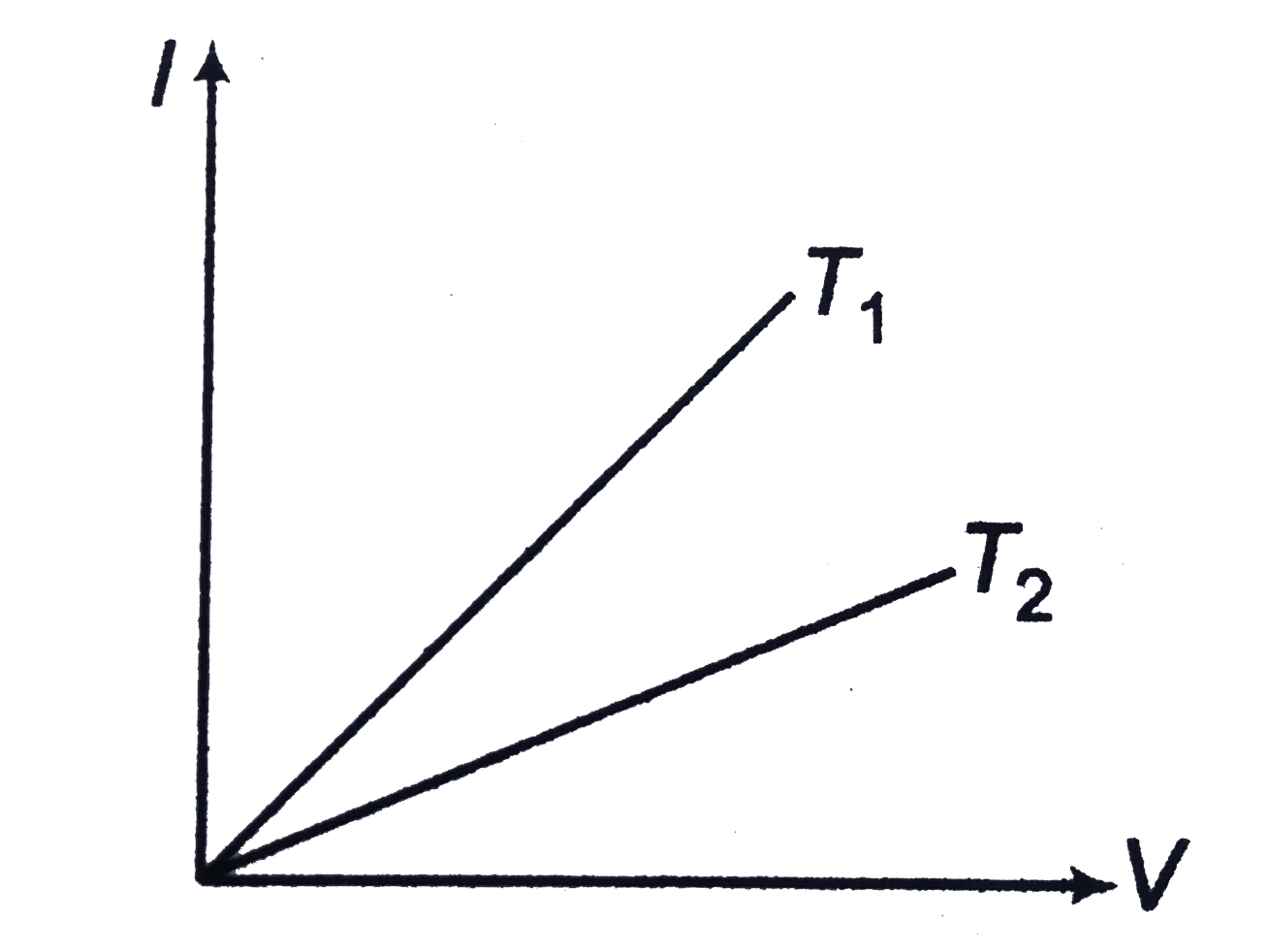 View Solution
View SolutionThe current voltage graphs for a given metalic wire two different temperature T1 and T2 are shown in figure The temperature T2 is greater than T1. Is this statement true or false?
 View Solution
View SolutionI-V graph for a metallie wire at two different tempearture, T1andT2 is as shown in the figure. Which of the two temperatures is lower and why ?
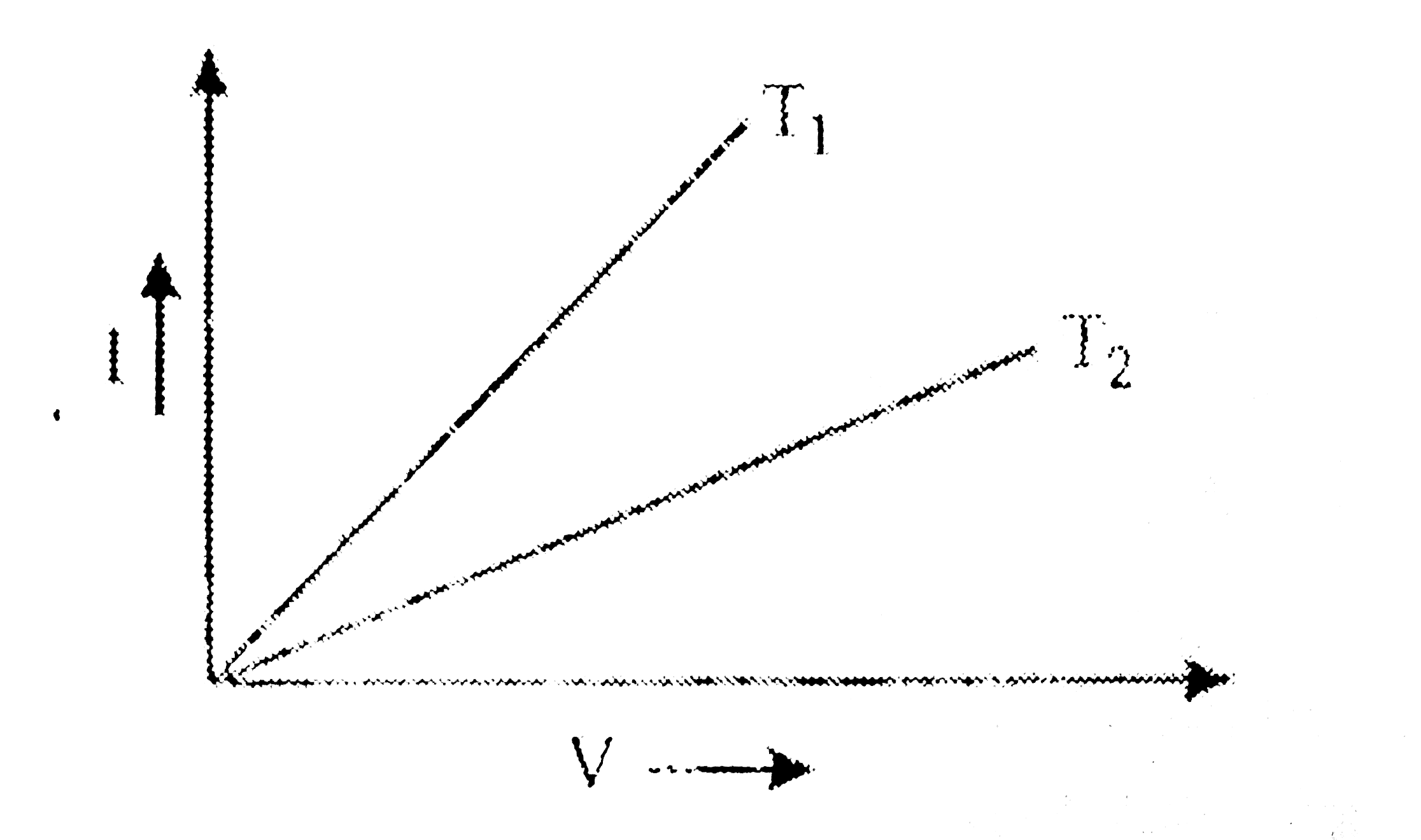 View Solution
View SolutionThe plots of intensity versus wavelength for three black bodies at temperatures T1,T2 and T3 respectively are shown in Their temperatures are shown in How their temperatures are related ?
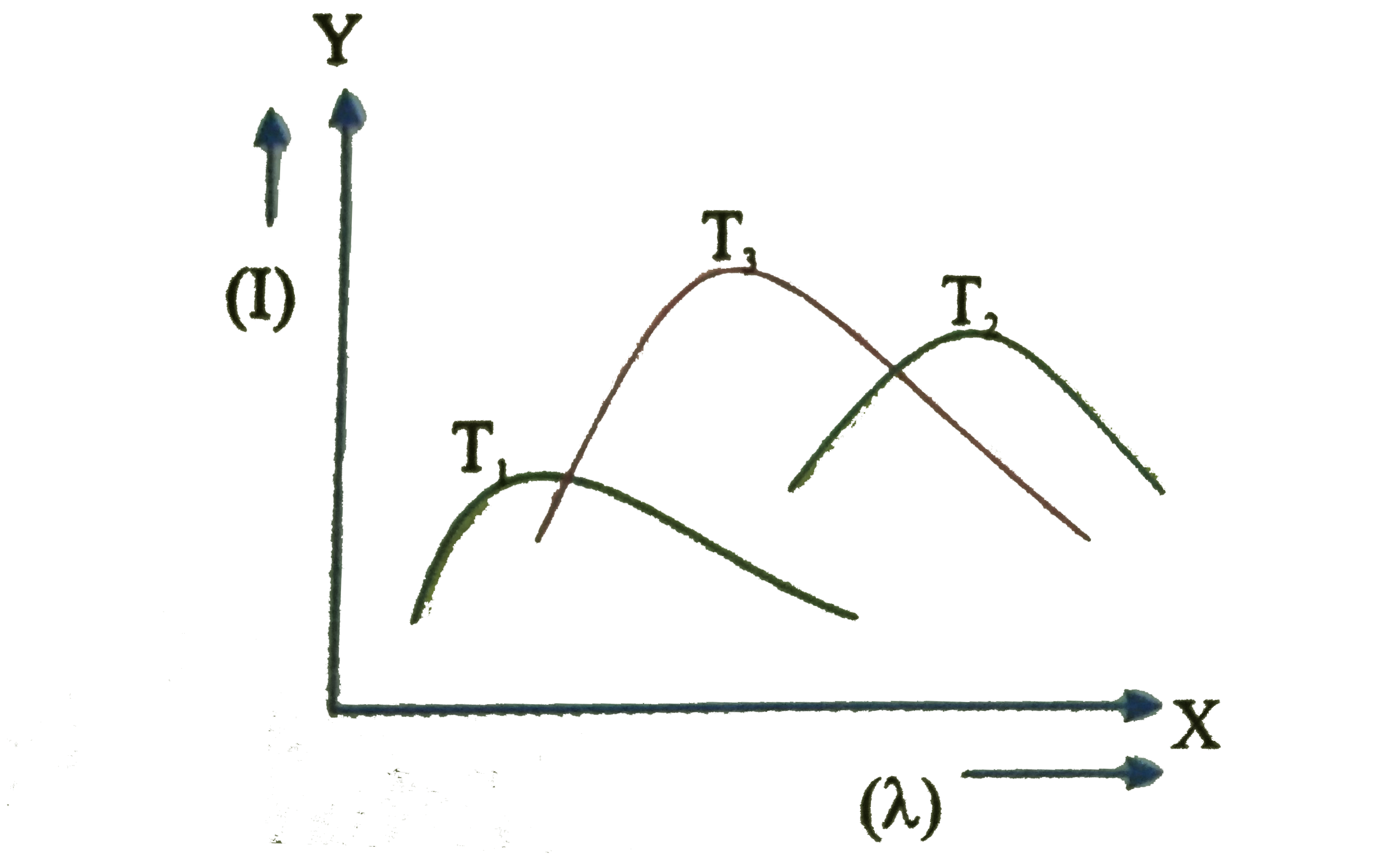 .View Solution
.View SolutionThe current - voltage graphs for a given metallic wire at two different temperatures T1andT2 are shown in the figure.
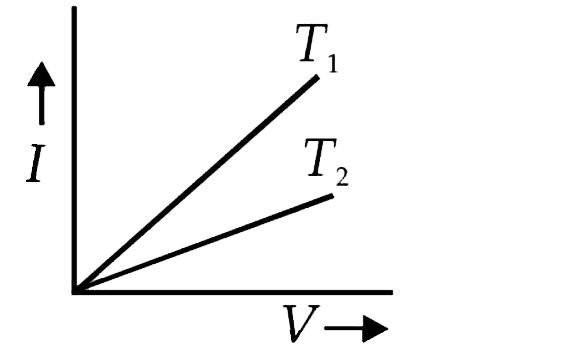
The temperature T2 is greater than T1.View Solution

