ABCD is a rhombus with AC=2BD. Diagonals AC and BD intersect at P.E1,E2,E3andE4 are four ellipes passing through P and their foci are A and B, B and C, C and D and D and A, respectively . If for i=1,2,3,4,ei are the eccentricities fo Ei, then
ei=e3
e2=e4
e1=2e2
e1=e2
To solve the problem, we need to analyze the properties of the rhombus ABCD and the ellipses defined by the points A, B, C, D, and the intersection point P of the diagonals AC and BD.
1. Understanding the Rhombus and its Diagonals:
- Let the diagonals AC and BD intersect at point P.
- Given that AC = 2BD, we can denote the lengths as follows:
- Let BD = 2x, then AC = 4x.
2. Properties of the Rhombus:
- In a rhombus, the diagonals bisect each other at right angles.
- Therefore, we have:
- AP = PC = 2x (since AC = 4x)
- BP = PD = x (since BD = 2x)
3. Foci of the Ellipses:
- The four ellipses E1, E2, E3, and E4 have the following foci:
- E1: Foci A and B
- E2: Foci B and C
- E3: Foci C and D
- E4: Foci D and A
4. Eccentricity of an Ellipse:
- The eccentricity e of an ellipse with foci at points F1 and F2 is given by:
e=da
where d is the distance between the foci and a is the semi-major axis length.
5. Calculating Eccentricities:
- For each ellipse, we can find the distance between the foci and the semi-major axis:
- E1: Foci A and B
- Distance AB=d1
- Semi-major axis a1=AP+PB=2x+x=3x
- Eccentricity e1=d1a1
- E2: Foci B and C
- Distance BC=d2
- Semi-major axis a2=BP+PC=x+2x=3x
- Eccentricity e2=d2a2
- E3: Foci C and D
- Distance CD=d3
- Semi-major axis a3=CP+PD=2x+x=3x
- Eccentricity e3=d3a3
- E4: Foci D and A
- Distance DA=d4
- Semi-major axis a4=DP+PA=x+2x=3x
- Eccentricity e4=d4a4
6. Conclusion on Eccentricities:
- Since the diagonals bisect each other and are equal in length, the distances between the foci for each ellipse will be equal.
- Therefore, we can conclude that:
e1=e2=e3=e4
7. Final Result:
- The eccentricities e1,e2,e3,e4 are equal, leading to the conclusion that:
- e1⋅e3=e2⋅e4 is true.
- Let the diagonals AC and BD intersect at point P.
- Given that AC = 2BD, we can denote the lengths as follows:
- Let BD = 2x, then AC = 4x.
- In a rhombus, the diagonals bisect each other at right angles.
- Therefore, we have:
- AP = PC = 2x (since AC = 4x)
- BP = PD = x (since BD = 2x)
- The four ellipses E1, E2, E3, and E4 have the following foci:
- E1: Foci A and B
- E2: Foci B and C
- E3: Foci C and D
- E4: Foci D and A
- The eccentricity e of an ellipse with foci at points F1 and F2 is given by:
e=da
where d is the distance between the foci and a is the semi-major axis length.
- For each ellipse, we can find the distance between the foci and the semi-major axis:
- E1: Foci A and B
- Distance AB=d1
- Semi-major axis a1=AP+PB=2x+x=3x
- Eccentricity e1=d1a1
- E2: Foci B and C
- Distance BC=d2
- Semi-major axis a2=BP+PC=x+2x=3x
- Eccentricity e2=d2a2
- E3: Foci C and D
- Distance CD=d3
- Semi-major axis a3=CP+PD=2x+x=3x
- Eccentricity e3=d3a3
- E4: Foci D and A
- Distance DA=d4
- Semi-major axis a4=DP+PA=x+2x=3x
- Eccentricity e4=d4a4
- Since the diagonals bisect each other and are equal in length, the distances between the foci for each ellipse will be equal.
- Therefore, we can conclude that:
e1=e2=e3=e4
- The eccentricities e1,e2,e3,e4 are equal, leading to the conclusion that:
- e1⋅e3=e2⋅e4 is true.
Similar Questions
In a rhombus ABCD the diagonals AC and BD intersect at the point (3,4) . If the point A is (1,2) the diagonal BD has the equation
View SolutionABCD is a rhombus. Its diagonals ACandBD intersect at the point M and satisfy BD=2AC.If he point DandM represent the complex numbers 1+iand2−i respectively, then A represents the complex number......or......
View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View SolutionIn quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE:EC=BE:ED.
Show that : ABCD is a trapezium.
View SolutionB (-5, 6) and D (1, 4) are the vertices of rhombus ABCD. Find the equations of diagonals BD and AC.
View SolutionIf a line intersects sides AB and AC of a ΔABCat D and E respectively and is parallel to BC, prove that ADAB=AEAC
View SolutionIf e1,e2,e3 and e4 are the four elementary outcomes in a sample space and P(e1)=0.1,P(e2)=0.5,and P(e3)=0.1, then the probability of e4 is ……
View SolutionIn Figure, the incircle of ABC touches the sides BC, CA and AB at D, E and F respectively. Show that AF+BD+CE=AE+BF+CD=12(Perimeter of ABC).
View SolutionA, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC =130∘ and ∠ECD=20∘ Find ∠BAC∘
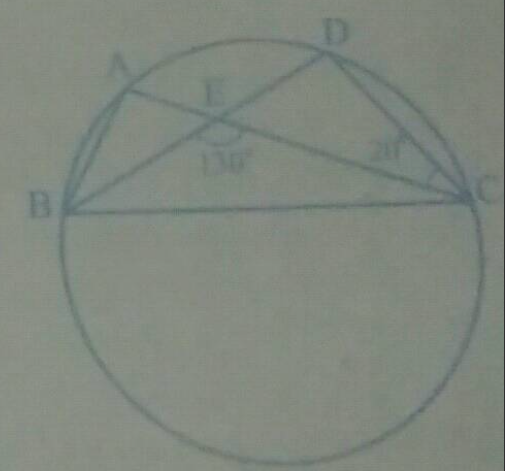
View SolutionThe vertices of ABC are A(4, 6), B(1, 5) and C(7, 2) . A line is drawn to intersect sides AB and AC at D and E respectively such that ADAB=AEAC=14 . Calculate the area of ADE and compare it with the area of ABC .
View Solution
