D and E are the mid-points of the sides AB and AC of ΔABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is Option1 a square Option2 a rectangle Option3 a rhombus Option4 a parallelogram
a square
a rectangle
a rhombus
a parallelogram
The correct Answer is:D
In ΔABC, D and E are the mid-points of sides AB and AC, respectively. ltBrgt By mid-point theorem,
DE∣∣BC
and DE=12BC ...(i)
Then, DE=12[BP+PO+OQ+QC] ltBrgt DE=12[2PO+2OQ]
[since, P and Q are the mid-points of OB and OC respectively]
⇒ DE=PO+OQ
⇒ DE=PQ
Now, in ΔAOC, Q and E are the mid-points of OC and AC respectively.
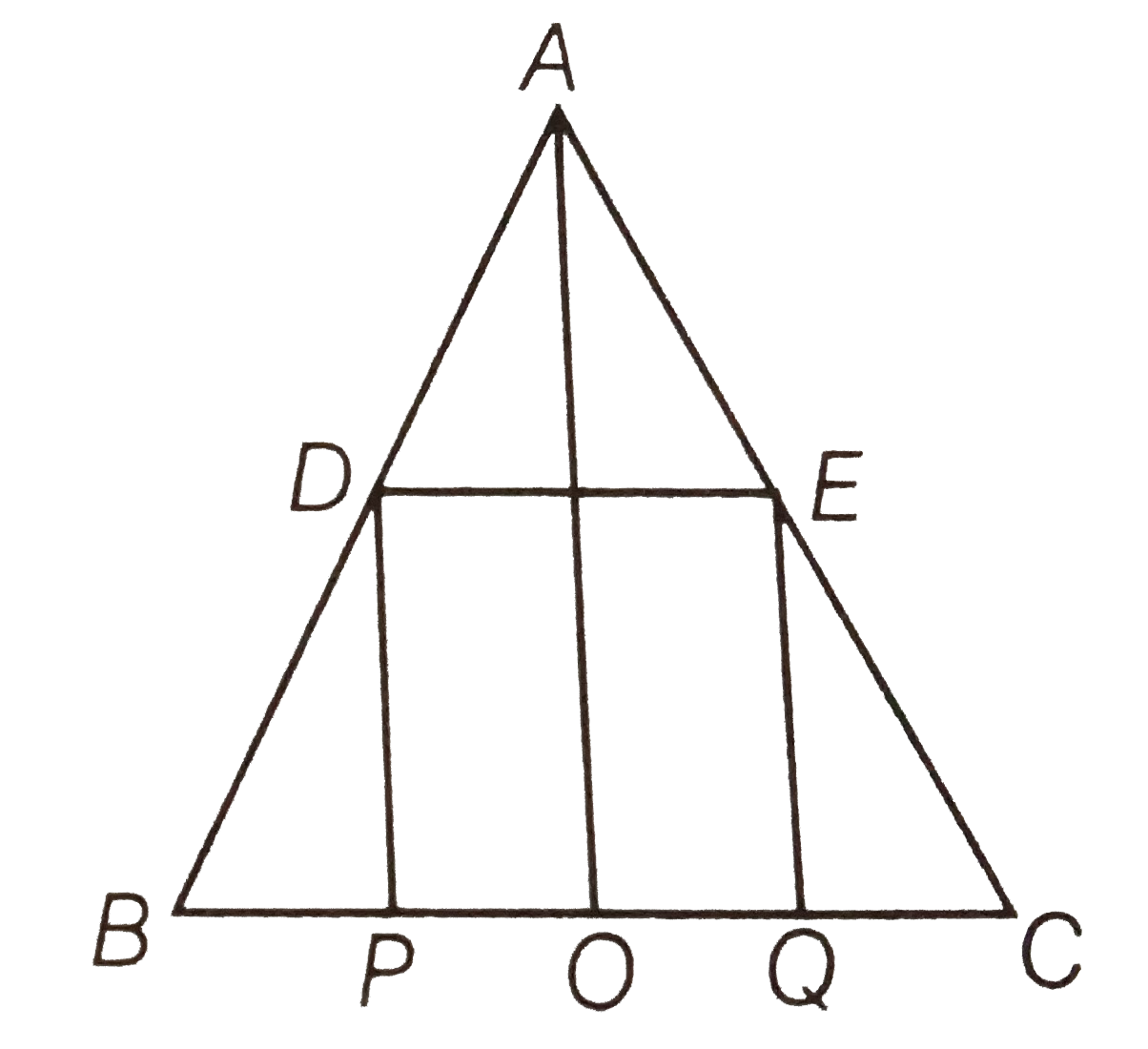
∴ EQ∣∣AOandEQ=12AO
[by mid-point theorem]...(iii)
Similarly, in ΔABO, PD∣∣AO and PD = 12AO
[by mid-point theorem]...(iv)
From Eqs. (iii) and (iv),
EQ∣∣PDandEQ=PD
From Eqs. (i) and (ii), DE∣∣BC(orDE∣∣PQ)andDE=PQ
Hence, DEQP is a parallelogram.
Topper's Solved these Questions
- QUADRILATERALS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
14 Videos
- QUADRILATERALS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - SHORT ANSWER TYPE QUESTIONS
10 Videos
- POLYNOMIALSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - POLYNOMIALSEXERCISE - EXERCISE 2.4 Long Answer type Questions
9 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
12 Videos
Similar Questions
D, E and F are the mid-points of the sides AB, BC and CA respectively of A ABC. AE meets DF at O. P and Q are the mid-points of OB and OC respectively. Prove that DPOF is a parallelogram.
View SolutionThe figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is Option1 a rhombus Option2 a rectangle Option3 a square Option4 any parallelogram
View SolutionIf P, Q , R are the mid-points of the sides AB, BC and CA of ΔABC and O is point whithin the triangle, then −−→OA+−−→OB+−−→OC=
View SolutionIf D id the mid-point of the side BC of a triangle ABC and AD is perpendicular to AC , then
View SolutionIf D,E and F are the mid-points of the sides BC,CA and AB, respectively of a ΔABC and O is any point, show that
(i) AD+BE+CF=0
(ii) OE+OF+DO=OA
View SolutionIf D,E and F are the mid-points of the sides BC,CA and AB respectively of the ΔABC and O be any point, then prove that OA+OB+OC=OD+OE+OF
View SolutionIf D and E are the mid-points of sides AB and AC of a triangle ABC respectively, show that →BE+→DC=32→BC.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionD and F are the mid-points of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
Find AB, if EF=4.8cm.
View Solution
