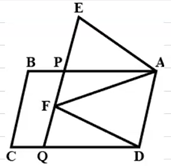
In the figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then, ar(ΔDPC)=12ar(EFGD).
Text Solution
False
In the given figure, join PG. Since, G is the mid-point of CD.
Thus, PG is a median of ΔDPC and it divides the triangle into parts of equal areas.
Then, ar(ΔDPG)=ar(ΔGPC)=12ar(ΔDPC) …(i)
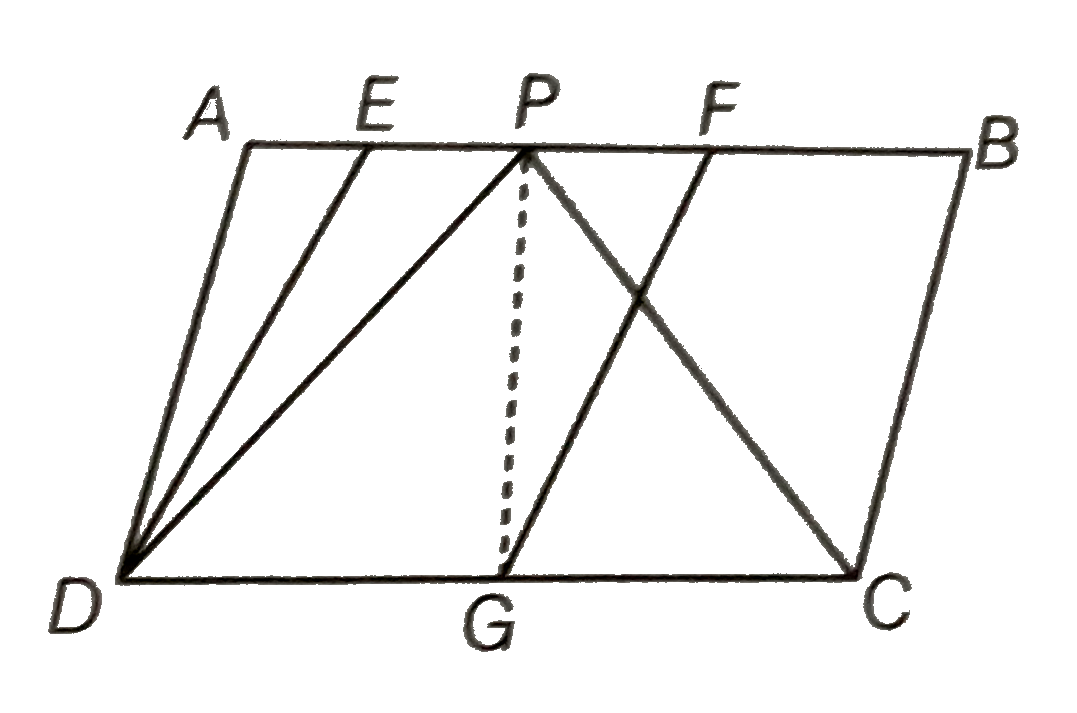
Also, we know that, if a parallelogram and a triangle lie on the same base and between the same parallels, then area of triangle is equal to half of the area of parallelogram.
Here, parallelogram EFGD and ΔDPG lie on the same base DG and between the same parallels DG and EF.
So, ar(ΔDPG)=12ar(EFGD) ...(ii)
From Eqs. (i) and (ii). 12ar(ΔDPC)=12ar(EFGD)
⇒ ar(ΔDPC)=ar(EFGD)
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.3 Short Answer Type Questions9videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions10videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions10videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.414videos
CIRCLES
Similar Questions
Knowledge Check
- Question 1 - Select One
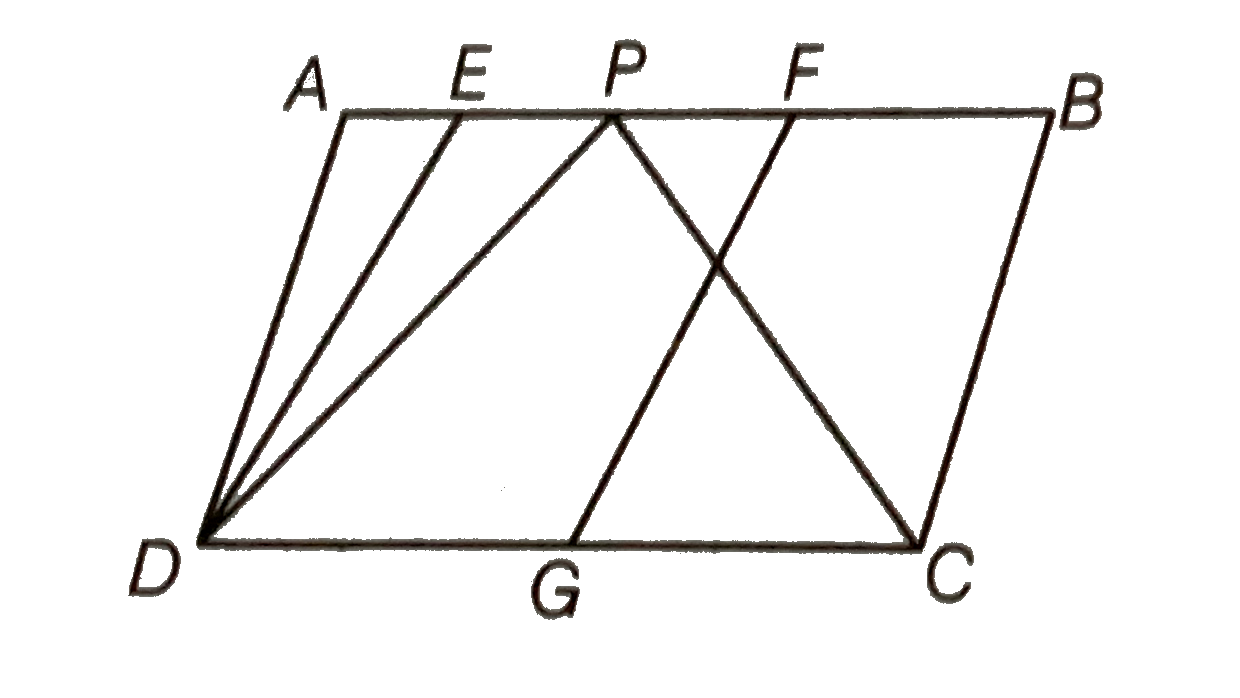
In the given figure, ABCD and AEFD a re two parallelograms.
ar(ΔPEA) =Aar(∣∣gmΔPEA)Bar(ΔPFD)Car(ΔQFD)Dar(∣∣gmΔCQPB) - Question 2 - Select One
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=12ar(ΔABC).
ATrueBFalseCPartially trueDNone of these - Question 3 - Select One
In the given figure, ABCD and AEFD a re two parallelograms.
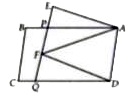
(ar(ΔAPE))/(ar(ΔPFA)) =A(ar(ΔQFD))/(ar(ΔPFD))B(ar(ΔAEF))/(ar(ΔPFD))C(ar(ΔQFD))/(ar(ΔAEF))DNone of these
ABCD is a parallelogram and X is the mid-point of AB. (AXCD)=24cm2, then ar(ABC)=24cm2.
View SolutionABCD is a parallelogram and X is the mid-point of AB. (AXCD)=24cm2, then ar(ABC)=24cm2.
View SolutionIn the figure ABCD and ABFE are Parallelograms then find ar (ΔBCF).
If ar (ABCE)=18cm2
ar (ABCD)=25cm2
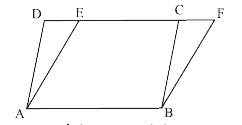 View Solution
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
View SolutionIn the figure, ABCD, DCFE and ABFE are parallelograms. Show that ar(ΔADE) = ar(ΔBCF).
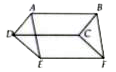 View Solution
View Solution