ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
Given ABCD is a parallelogram. A circle whose centre O passes through A, B is so drawm that it intersect AD at P and BC at Q
To prove Points P, Q, C and D are con-cyclic.
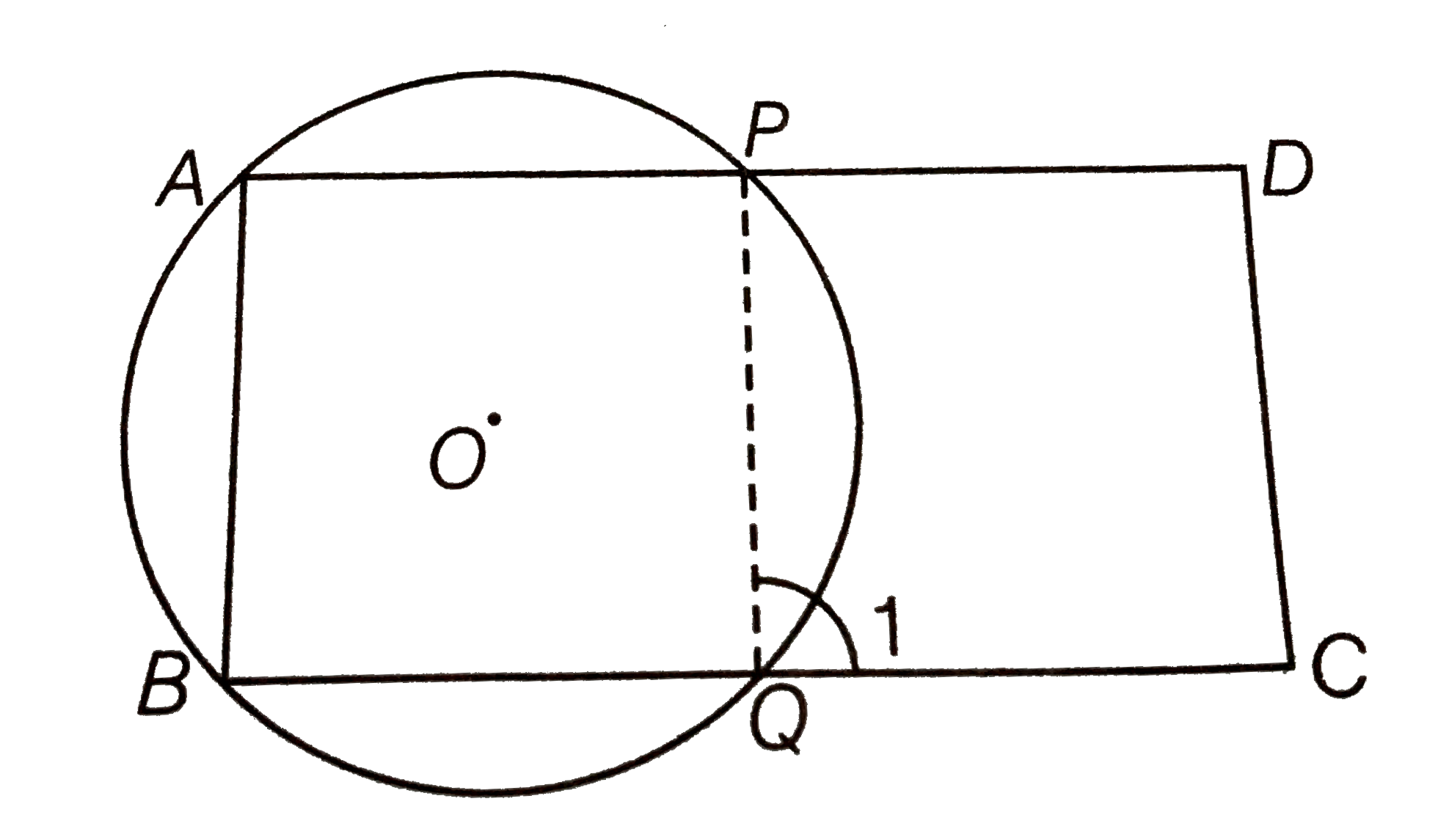
Construction Join PQ
Proof ∠1=∠A [exterior angle property of cyclic quadrilateral]
But∠A=∠C [opposite angles of a parallelogram]
∴∠1=∠C ...(i)
But ∠C=∠D=180∘
[sum of cointerior angles on same side is 180∘]
⇒∠1+∠D=180∘ [from Eq. (i)]
Thus, the quadrilateral QCDP is cyclic.
So, the points P, Q ,C and D are con-cyclic.
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.3
20 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
The diagonals of a parallelogram ABCD intersect at a point O. Through O, a line a drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O , a time is drawn to intersect AD at P and BC at Q . Show that PQ divides the parallelogram into two parts of equal area.
View SolutionP is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
View SolutionABCD is a parallelogram . The circle passing through the vertices. A, B and C intersects CD (or CD produced) at E. Prove that AE=AD.
View SolutionABCD is a parallelogram, a line through A cuts DC at point P and BC produced at Q.
Prove that triangle BCP is equal in area to triangle DPQ.
View SolutionABCD is a parallelogram, a line through A cuts DC at point P and BC produced at Q.
Prove that triangle BCP is equal in area to triangle DPQ.

View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(POA)=ar(QOC).
View SolutionA circle intersects the side AD of a parallelogram ABCD at P and BC produced at Q. Prove that square PDQC is cyclic .
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
View Solution