A circle has radius √2cm it is divided into 2 segments by a chord of length 2cm prove that angle subtended by the chord at a point in major segment is 45∘
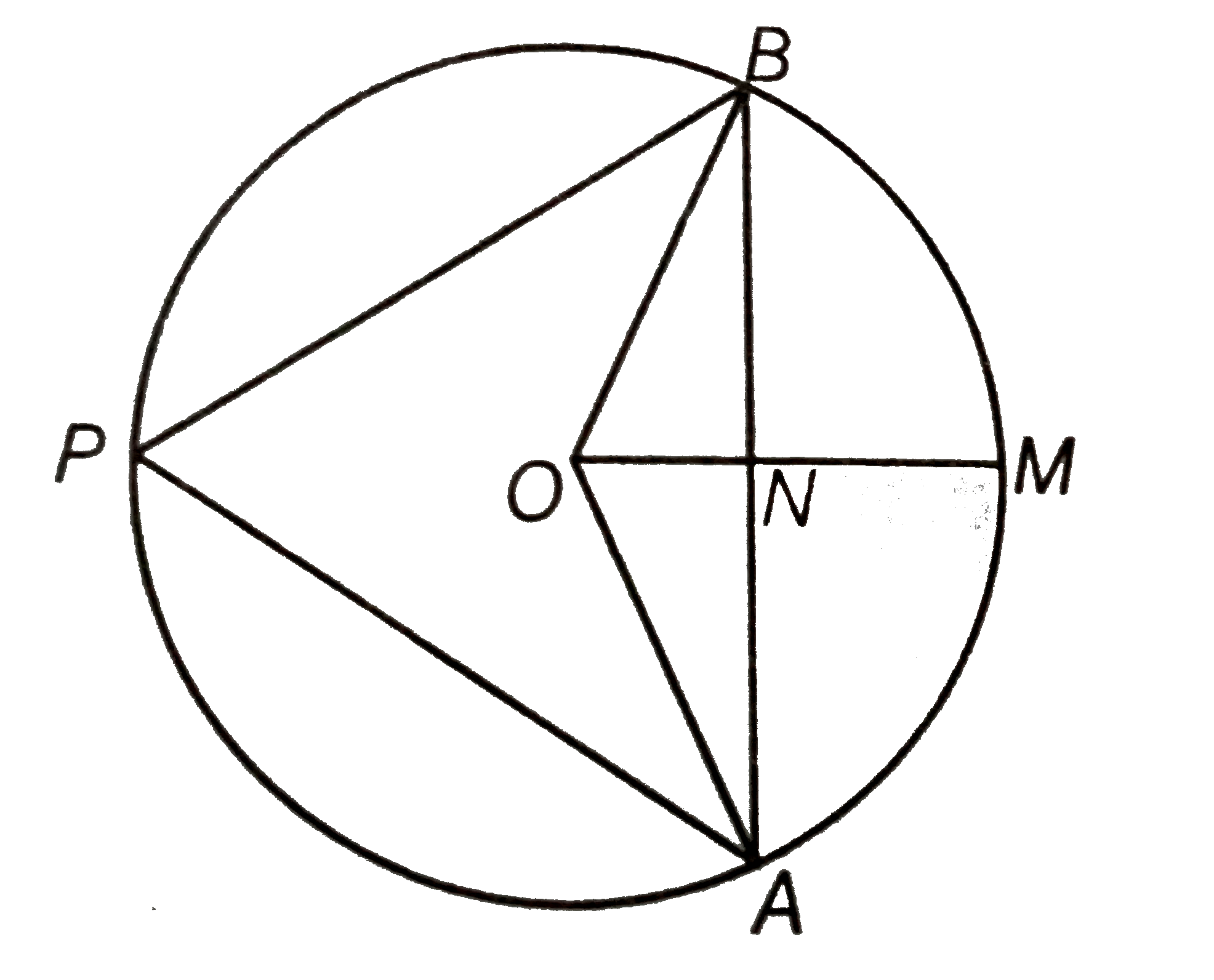
Draw a circle having centre O. Let AB=2 cm be a chord of a circle. A chord AB is divided by the line OM in two equal segments.
To prove ∠APB=45∘
Here, AN=NB = 1 cm
and OB=√2cm
In ΔONB,OB2=ON2+NB2
[use Pythagoras theorem]
⇒(√2)2=ON2+(1)2
⇒ON2=2−1=1
⇒ON=1cm
[taking positive square root, because distance is always positive]
Also, ∠ONB=90∘ [ON is the perpendicular bisector of the chord AB]
∴∠NOB=∠NBO=45∘
Similarly, ∠AON=45∘
Now, ∠AOB=∠AON+∠NOB
=45∘+45∘=90∘
We know that, chord subtends an angle to the circle is half the angle subtended by it to the centre.
∴∠APB=12∠AOB
=90∘2=45∘
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.3
20 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
A circle has radius 7 cm. What is the length of its longest chord ?
View SolutionA circle has radius 4cm. What is the length of its longest chord?
View SolutionA circle has radius 5cm. What is the length of its longest chord?
View SolutionIf the chord of a circle is equal to the radius of the circle, then the angle subtended by the chord at a point on the minor arc is .........
View SolutionProve that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
View SolutionDivide a line segment of length 10cm internally in the ratio 3:2
View SolutionDivide a line segment of length 5 cm externally in the ratio 5:2 .
View SolutionDivide a line segment of length 8 cm internally in the ratio 4:2 .
View SolutionThe chord of a circle is equal to its radius, find the angle subtended by this chord at the centre.
View SolutionA chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
View Solution
