Which of the following is not the graph of a quadratic polynomial?
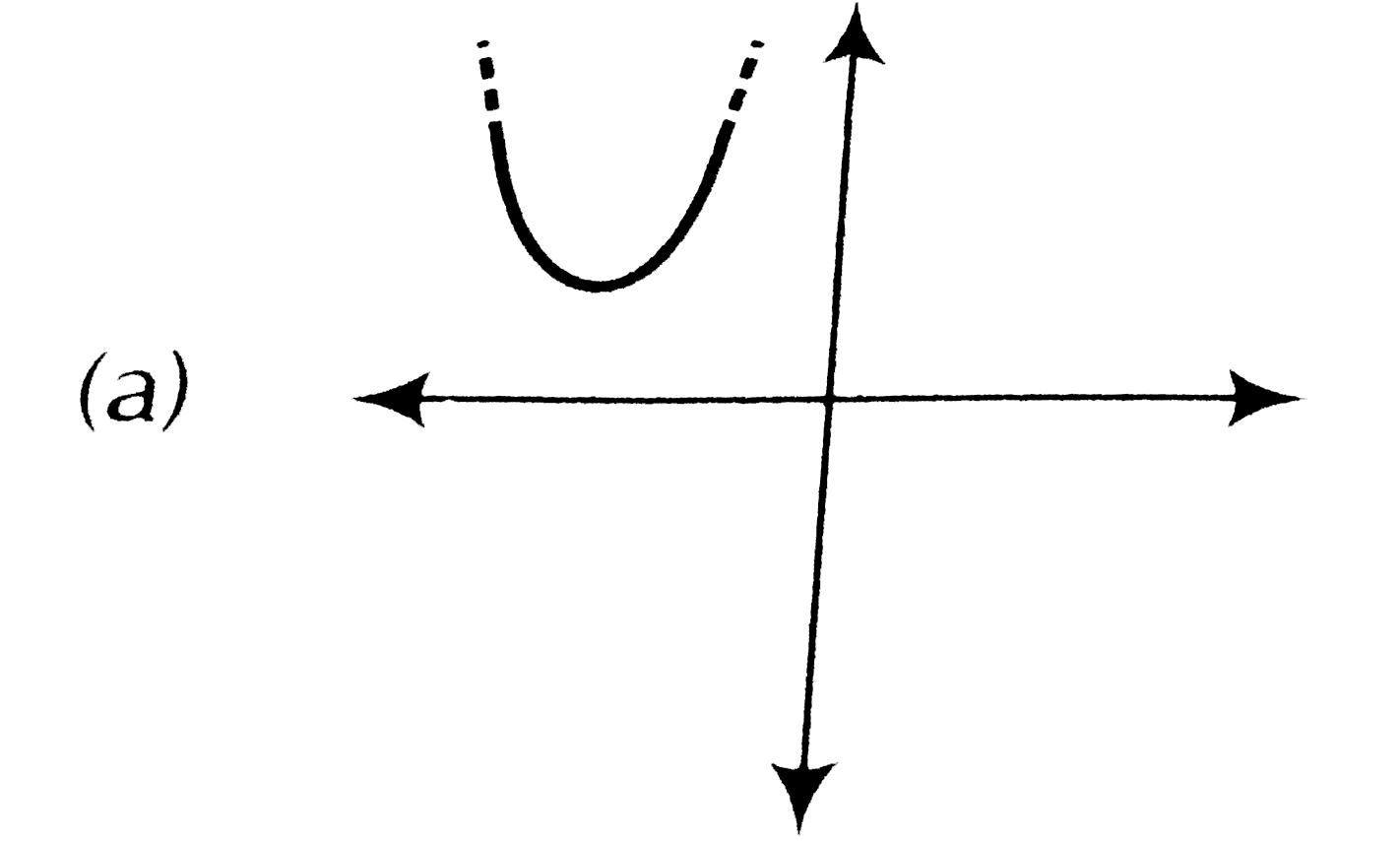
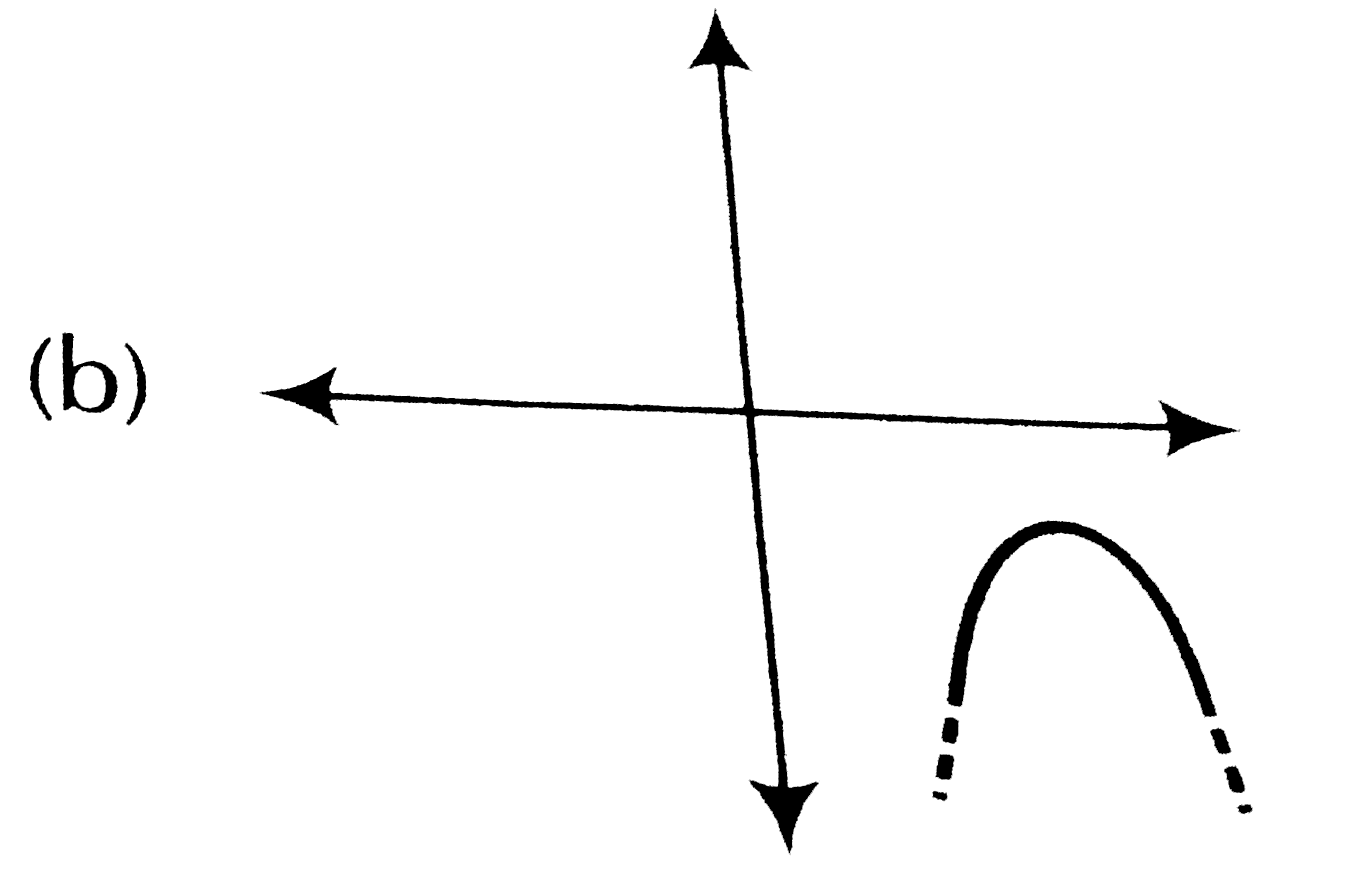
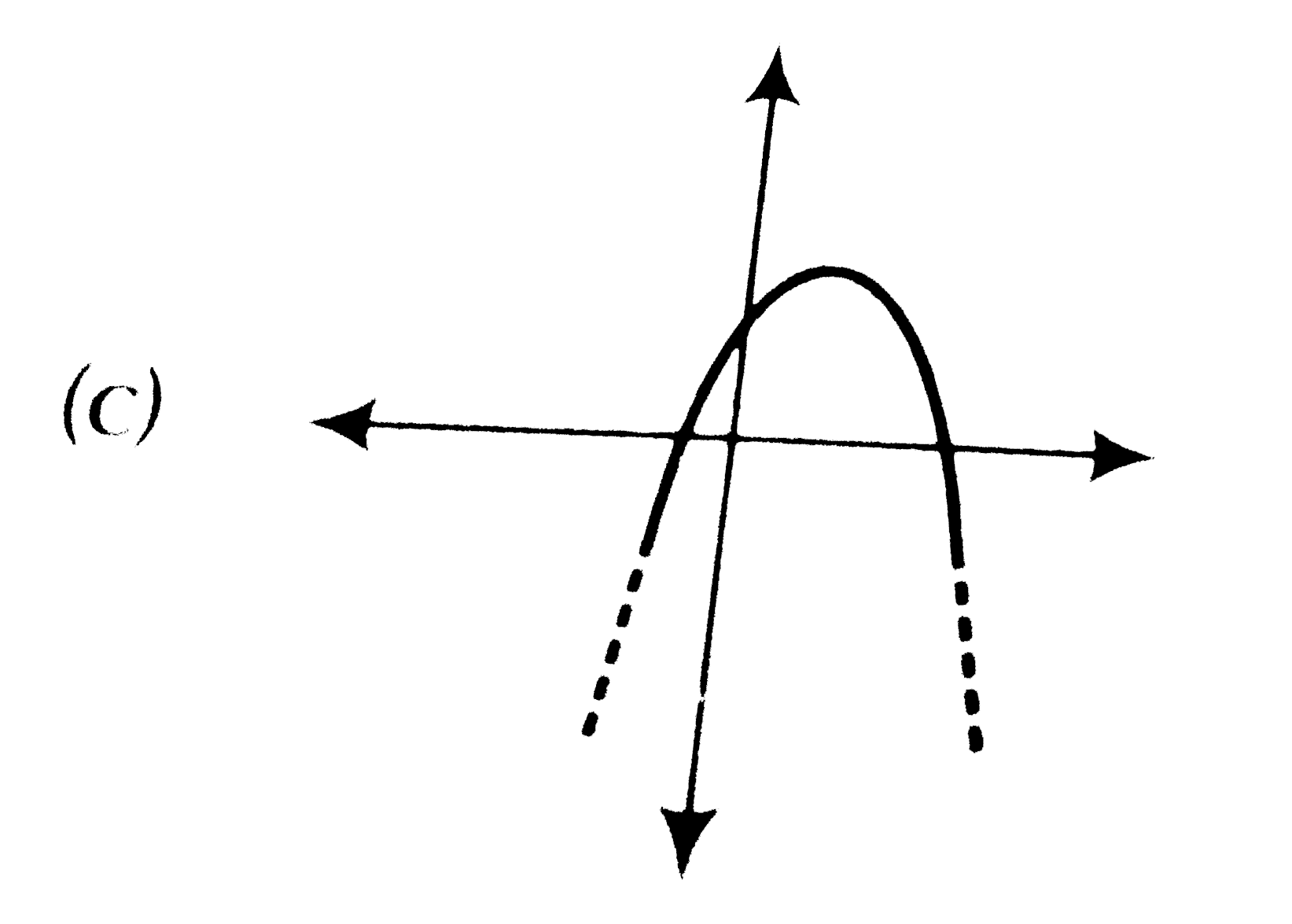
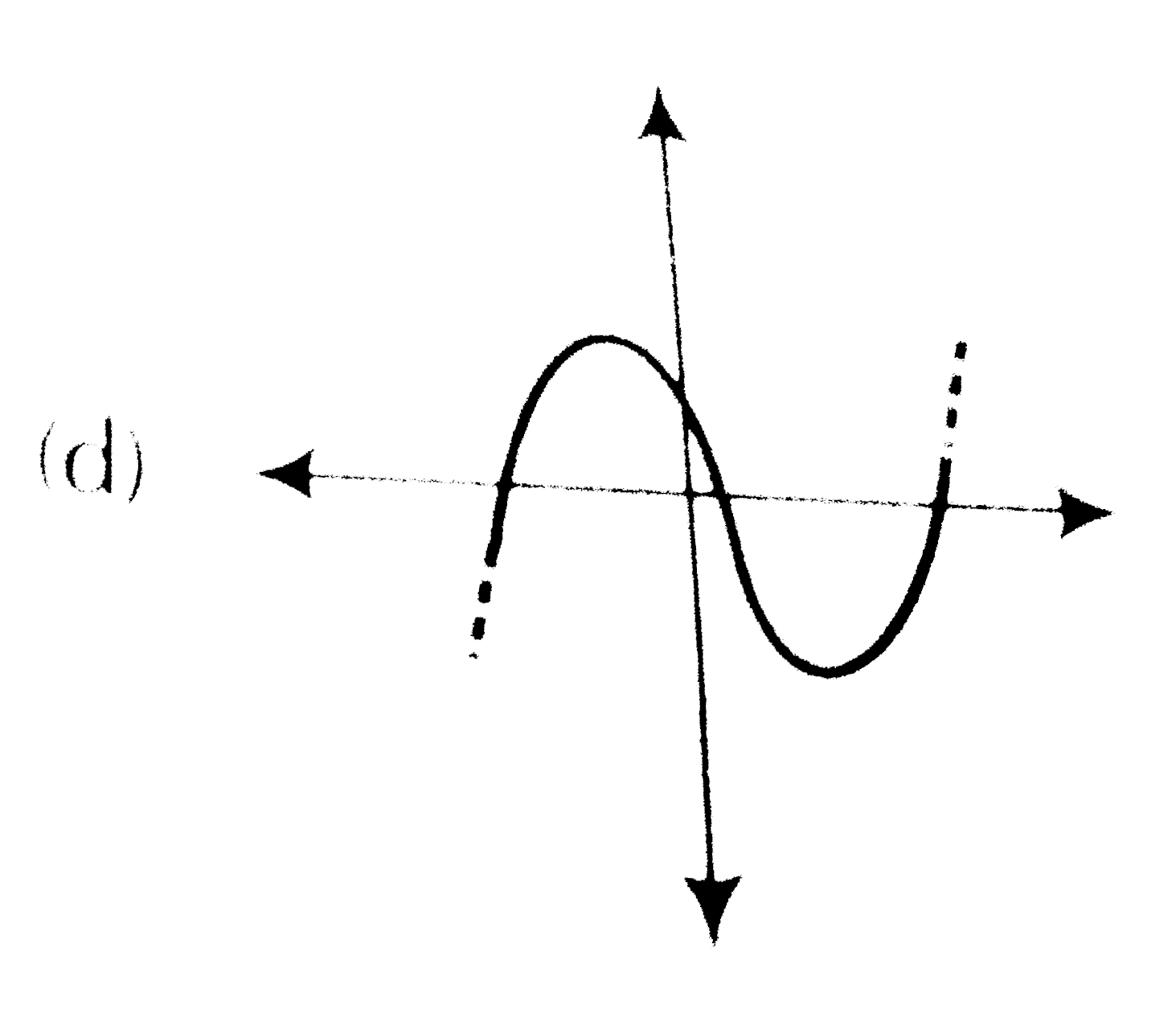
The correct Answer is:D
To determine which of the given graphs is not the graph of a quadratic polynomial, we need to understand the characteristics of quadratic polynomials and their graphs.
1. Understanding Quadratic Polynomials:
A quadratic polynomial is generally expressed in the form ax2+bx+c, where a,b, and c are constants and a≠0. The graph of a quadratic polynomial is a parabola.
Hint: Remember that the standard form of a quadratic polynomial is ax2+bx+c.
2. Roots of Quadratic Polynomials:
A quadratic polynomial can have at most 2 real roots. This means that the graph can intersect the x-axis at either 0, 1, or 2 points.
Hint: Consider the maximum number of intersections a parabola can have with the x-axis.
3. Shape of the Graph:
The graph of a quadratic polynomial can open upwards or downwards, depending on the sign of the coefficient a:
- If a>0, the parabola opens upwards.
- If a<0, the parabola opens downwards.
Hint: Check the direction of the parabola to determine the sign of a.
4. Analyzing the Given Graphs:
- Graph 1: This graph touches the x-axis at two points (two equal roots). This is a valid quadratic polynomial.
- Graph 2: This graph intersects the x-axis at two distinct points (two distinct roots). This is also a valid quadratic polynomial.
- Graph 3: This graph intersects the x-axis at three points. Since a quadratic polynomial cannot have more than 2 real roots, this graph cannot represent a quadratic polynomial.
Hint: Count the number of points where each graph intersects the x-axis.
5. Conclusion:
Based on the analysis, the graph that intersects the x-axis at three points is not the graph of a quadratic polynomial.
Final Answer:
The graph that intersects the x-axis at three points is not the graph of a quadratic polynomial.
A quadratic polynomial is generally expressed in the form ax2+bx+c, where a,b, and c are constants and a≠0. The graph of a quadratic polynomial is a parabola.
A quadratic polynomial can have at most 2 real roots. This means that the graph can intersect the x-axis at either 0, 1, or 2 points.
The graph of a quadratic polynomial can open upwards or downwards, depending on the sign of the coefficient a:
- If a>0, the parabola opens upwards.
- If a<0, the parabola opens downwards.
- Graph 1: This graph touches the x-axis at two points (two equal roots). This is a valid quadratic polynomial.
- Graph 2: This graph intersects the x-axis at two distinct points (two distinct roots). This is also a valid quadratic polynomial.
- Graph 3: This graph intersects the x-axis at three points. Since a quadratic polynomial cannot have more than 2 real roots, this graph cannot represent a quadratic polynomial.
Based on the analysis, the graph that intersects the x-axis at three points is not the graph of a quadratic polynomial.
The graph that intersects the x-axis at three points is not the graph of a quadratic polynomial.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - POLYNOMIALS EXERCISE - Very Short Answer Type Questions2videos
POLYNOMIALS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - POLYNOMIALS EXERCISE - Short Answer Type Questions10videos
POLYNOMIALS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PAIR OF LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Exercise 3.4 Long Answer Type Questions13videos
PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRIATIC EQUATIONSEXERCISE - LONG ANSWER TYPE12videos
QUADRIATIC EQUATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following graphs could not be the graph of a function?
A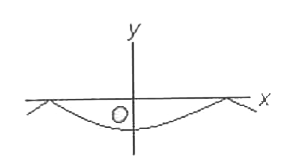 B
B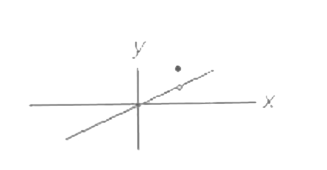 C
C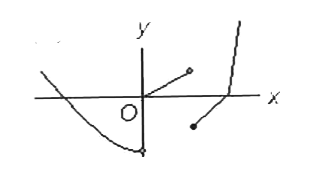 D
D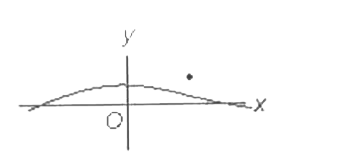
- Question 2 - Select One
A certain polynomial,P, has a degree of 2. Polynomial P has zeroes of 2 and -3 and a>0 when the function of polynomial P is written in the form of y=ax2+bx+c. Given this information, which of the following could be the graph of polynomial P?
A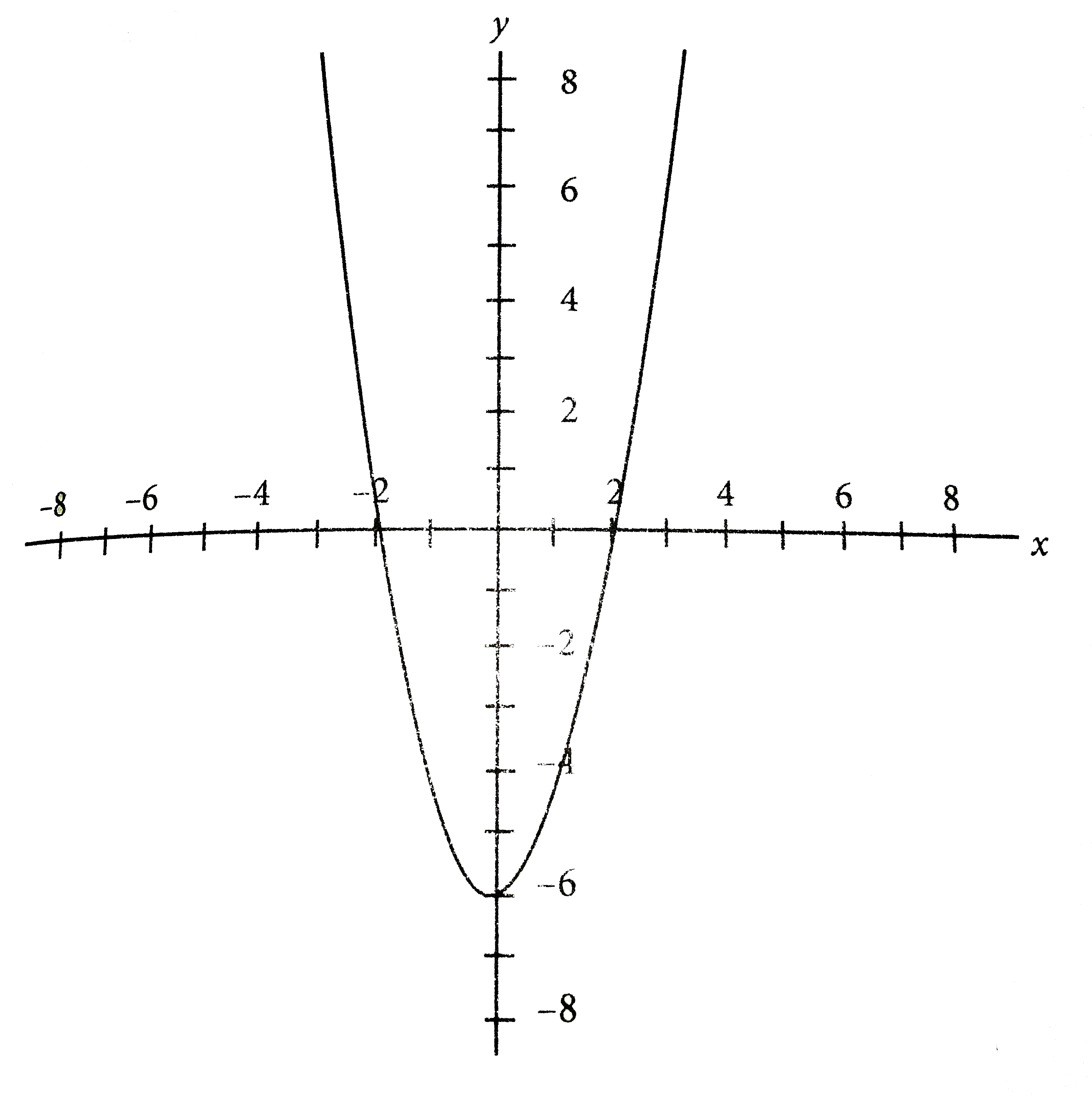 B
B C
C D
D
- Question 3 - Select One
Which of the following graphs is NOT a function ?
A B
B C
C D
D
Which of the following graphs are graphs of a function?

 View Solution
View SolutionIf each one of the following graphs is the graph of a polynomial, then identify which one corresponds to a linear polynomial and which one corresponds to a quadratic polynomial? (FIGURE)
View SolutionDraw the graph of the quadratic polynomial f(x)=3−2x−x2
View SolutionFor each of the following find a quadratic polynomial whose sum and product respectively of the zeroes are as given. Also, find the zeroes of these polynomials by factorisation. (i) −83,43 (ii) −32√5,−12
View SolutionWhich of the following is a quadratic equation?
View Solution

