If ΔABC~ΔEDF and ΔABC is npot similar to ΔDEF, then which of the following is not true?
BC⋅EF=AC⋅FD
AB⋅EF=AC⋅DE
BC⋅DE=AB⋅EF
BC⋅DE=AB⋅FD
To solve the problem, we need to analyze the given information about the similarity of triangles and determine which statement is not true based on the properties of similar triangles.
1. Understanding Triangle Similarity:
- We are given that triangle ABC is similar to triangle EDF (ΔABC ~ ΔEDF).
- This means that the corresponding angles are equal: ∠A = ∠E, ∠B = ∠D, and ∠C = ∠F.
- The sides of the triangles are in proportion:
ABDE=BCEF=ACDF
2. Analyzing the Statements:
- We need to evaluate each option provided in the question to find which one is not true.
3. Option A:
- Statement: BC⋅EF=AC⋅FD
- From the similarity, we have:
BCFD=ACEF
- Cross-multiplying gives:
BC⋅EF=AC⋅FD
- This statement is true.
4. Option B:
- Statement: AB⋅EF=AC⋅DE
- From the similarity, we have:
ABDE=ACEF
- Cross-multiplying gives:
AB⋅EF=AC⋅DE
- This statement is true.
5. Option C:
- Statement: BC⋅DE=AB⋅EF
- From the similarity, we have:
BCDF=ABED
- Cross-multiplying gives:
BC⋅ED=AB⋅DF
- The statement claims BC⋅DE=AB⋅EF, which does not match what we derived. Therefore, this statement is not true.
6. Conclusion:
- The statement that is not true is Option C: BC⋅DE=AB⋅EF.
- We are given that triangle ABC is similar to triangle EDF (ΔABC ~ ΔEDF).
- This means that the corresponding angles are equal: ∠A = ∠E, ∠B = ∠D, and ∠C = ∠F.
- The sides of the triangles are in proportion:
ABDE=BCEF=ACDF
- We need to evaluate each option provided in the question to find which one is not true.
- Statement: BC⋅EF=AC⋅FD
- From the similarity, we have:
BCFD=ACEF
- Cross-multiplying gives:
BC⋅EF=AC⋅FD
- This statement is true.
- Statement: AB⋅EF=AC⋅DE
- From the similarity, we have:
ABDE=ACEF
- Cross-multiplying gives:
AB⋅EF=AC⋅DE
- This statement is true.
- Statement: BC⋅DE=AB⋅EF
- From the similarity, we have:
BCDF=ABED
- Cross-multiplying gives:
BC⋅ED=AB⋅DF
- The statement claims BC⋅DE=AB⋅EF, which does not match what we derived. Therefore, this statement is not true.
- The statement that is not true is Option C: BC⋅DE=AB⋅EF.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Very Short Answer Typw Questions12videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Short Answer Type Questions15videos
TRIANGLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS20videos
SURFACE AREAS AND VOLUMES
Similar Questions
Knowledge Check
- Question 1 - Select One
What is the perimeter of ΔABC shown in the figure?
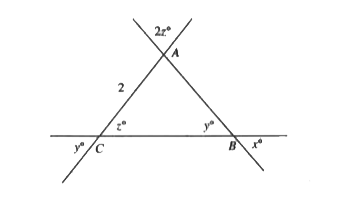 A2+4√2B4+2√2C8D4+4√2
A2+4√2B4+2√2C8D4+4√2
Which of the following is possible in ΔABC?
View SolutionIf ΔABC~ΔDFE,∠A=30,∠C=50∘,AB=5 cm,AC=8 cm and DF=7.5 cm. Then, which of the following is true?
View SolutionIn a ΔABC, sinAsinBsinC is
View SolutionIn a ΔABC,iftanA+2tanB=0, then which one is correct?
View SolutionIf a ΔABC is right angled at B, then the diameter of the incircle of the triangle is
View SolutionIn any ΔABC, is 2cosB=ac, then the triangle is
View SolutionIn ΔABC, prove that: sinB+sinC>sinA
View Solution

