In figure, AB and CD are common tangents to two circles of equal radii. Prove that AB=CD.

Given AB and CD are tangents to two circles of equal radii.
To prove AB=CD
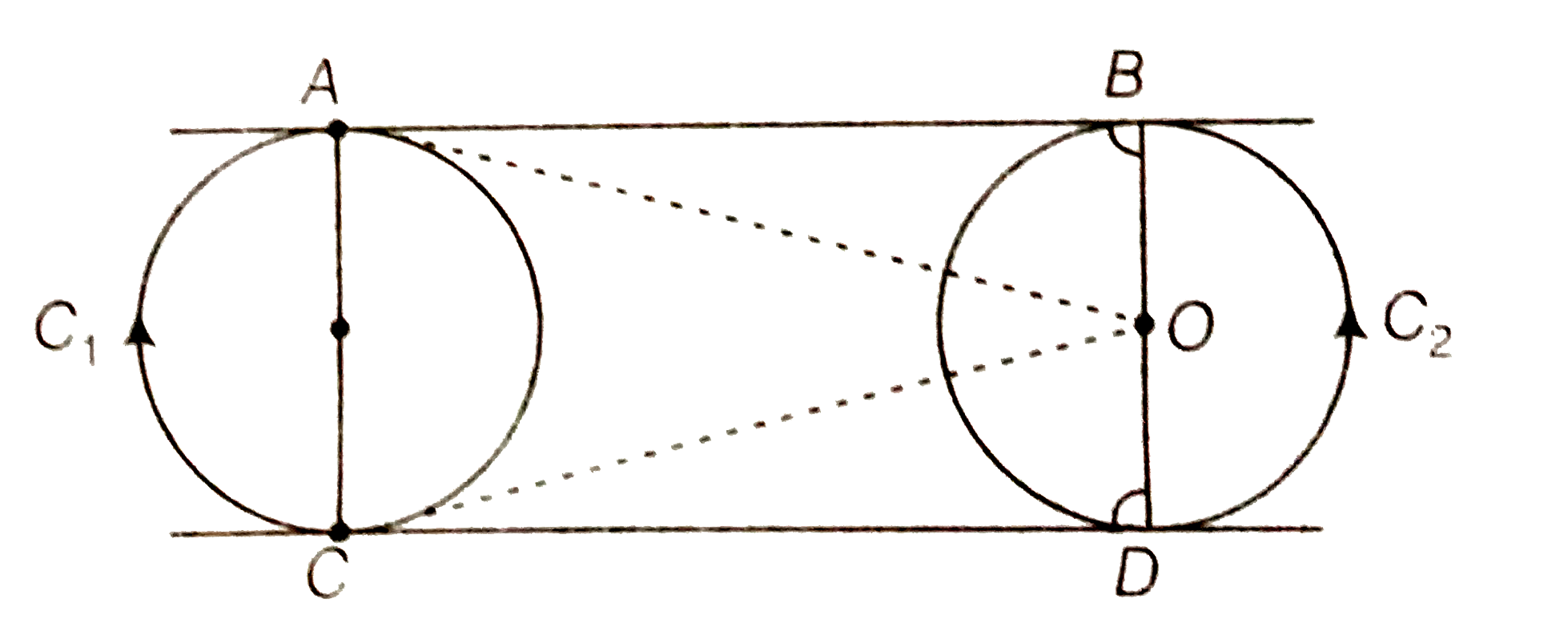
Construction Join OA, OC, O' B and O'D
Proof Now, ∠OAB=90∘
[tangent at any point of a circle is perpendicular to radius through the point of contact]
Thus, AC is a straight line.
Also, ∠OAB+∠OAB=180∘
∴AB/CD
Similarly, BD is a straight line
and ∠O'BA=∠O'DC=90∘
Also, AC=BD [radii of two circles are equal]
In quadrilateral ABCD, ∠A=∠B=∠C=∠D=90∘
and AC=BD
ABCD is a rectangle
Hence, AB=CD [opposite sides of rectangle are equal]
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS14videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.2 VERY SHORT ANSWER TYPE QUESTIONS10videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions10videos
ARITHMETIC PROGRESSIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the figure, AB and CD are the diameters of the circle. What is the value of x?
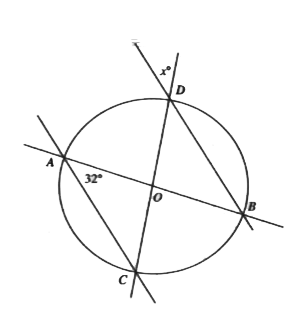 A16∘B18∘C26∘D32∘
A16∘B18∘C26∘D32∘
In the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.
 View Solution
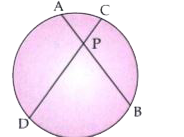
View SolutionAB and CD are two chords of a circle intersecting at P. Prove that AP×PB=CP×PD
 View Solution
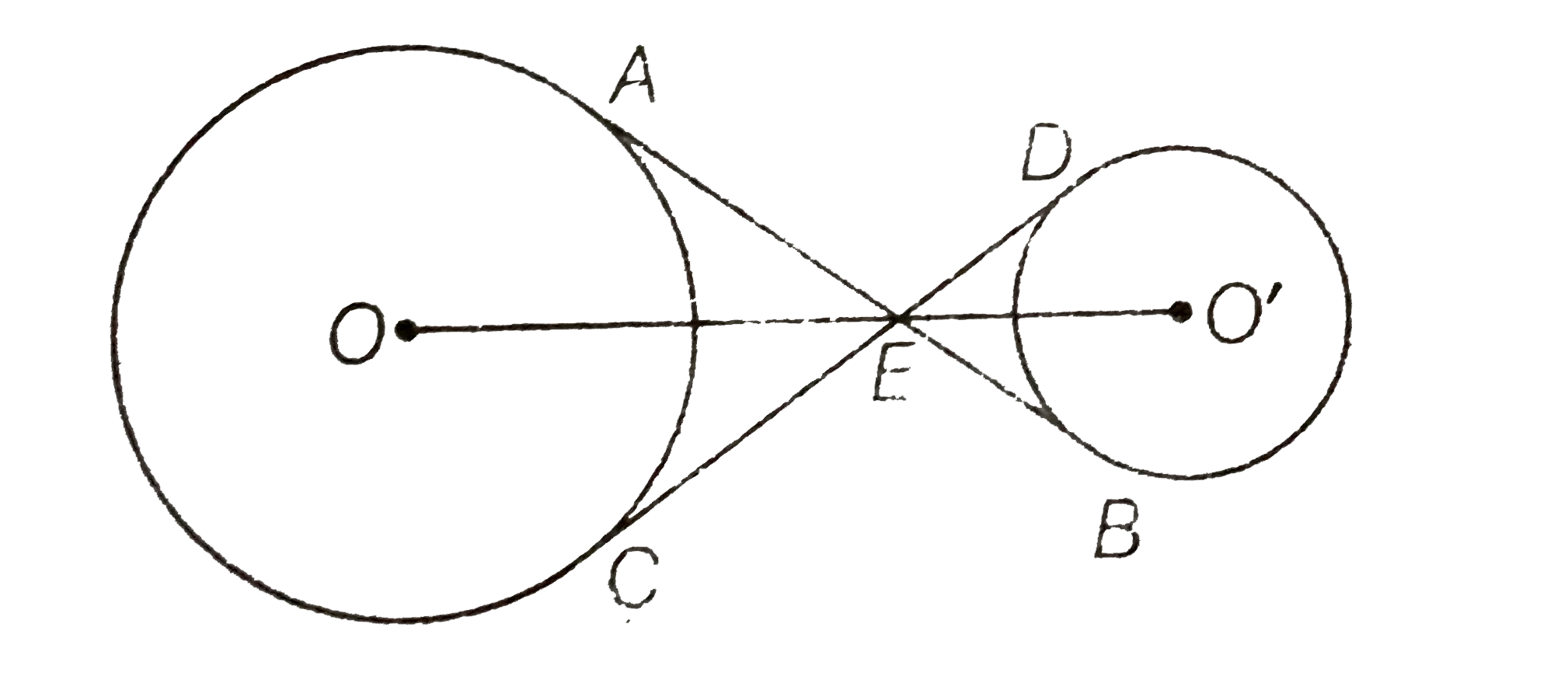
View SolutionIn a figure the common tangents, AB and CD to two circles with centers O and O' intersect at E. Prove that the points O, E and O' are collinear.
 View Solution
View SolutionIn the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that:
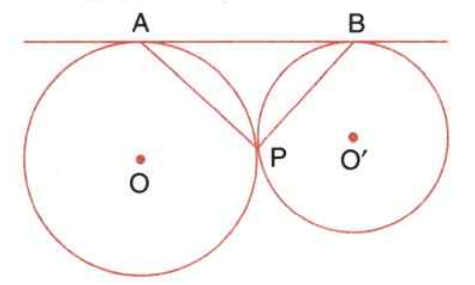
(i) tangent at point P bisects AB
(ii) angle APB=90∘View SolutionIn Figure, a quadrilateral ABCD is drawn to circumscribe a circle .
Prove that
AB+CD=BC+AD
 View Solution
View SolutionIn Figure, a quadrilateral ABCD is drawn to circumscribe a circle .
Prove that
AB+CD=BC+AD
 View Solution
View SolutionIn Figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘
View Solution



