In figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.

Given Common tangents AB and CD to two circles interescting at E.
To prove A
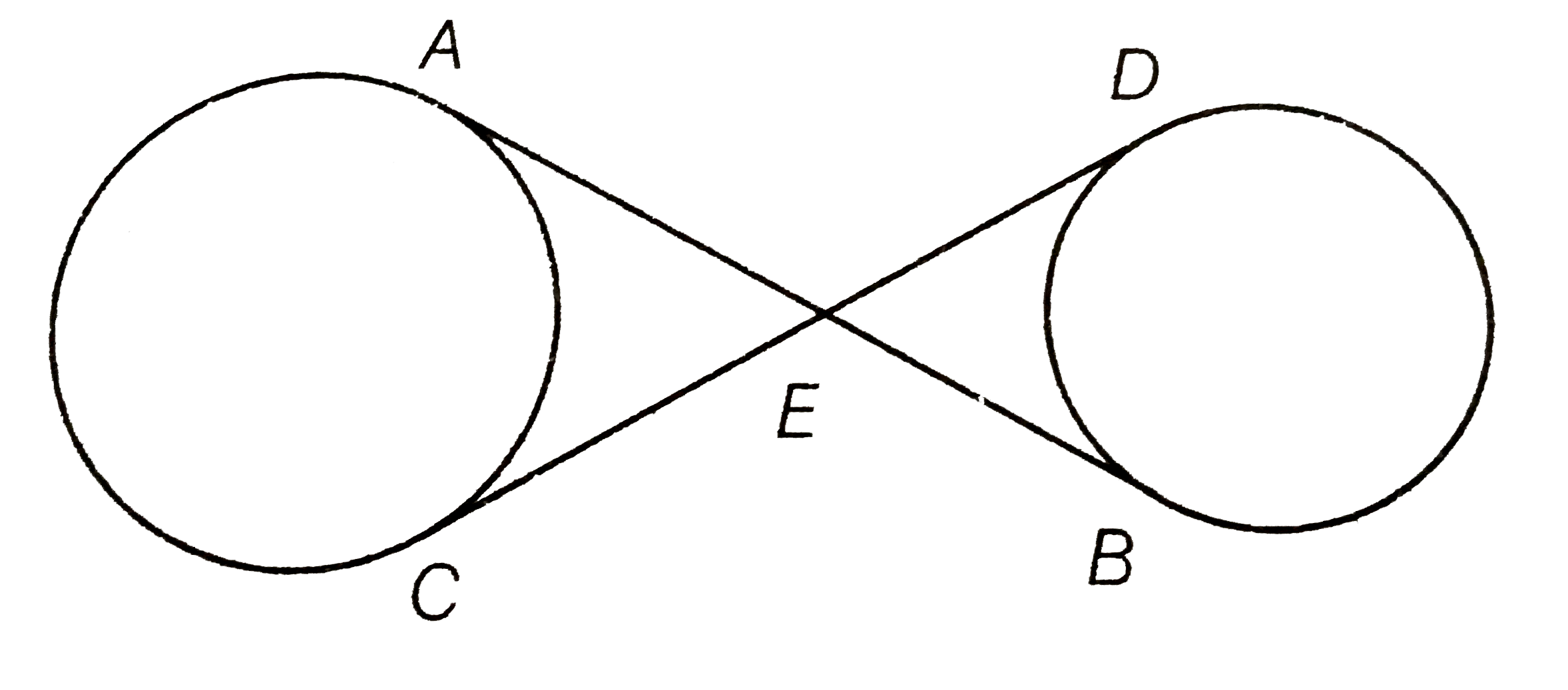
Proof EB=ED…..(i)
[the lengths of tangents drawn from an internal point to a circle are equal]
EB=ED......(ii)
On adding Eqs. (i) and (ii), we get
EA+EB=EC+ED
⇒AB=CD Hence proved.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS14videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.2 VERY SHORT ANSWER TYPE QUESTIONS10videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions10videos
ARITHMETIC PROGRESSIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
Similar Questions
In the adjoining figure, common tangents AB and CD to two circles intersect at P.
Prove that AB=CD.
 View Solution
View SolutionIn figure, AB and CD are common tangents to two circles of equal radii. Prove that AB=CD.
 View Solution
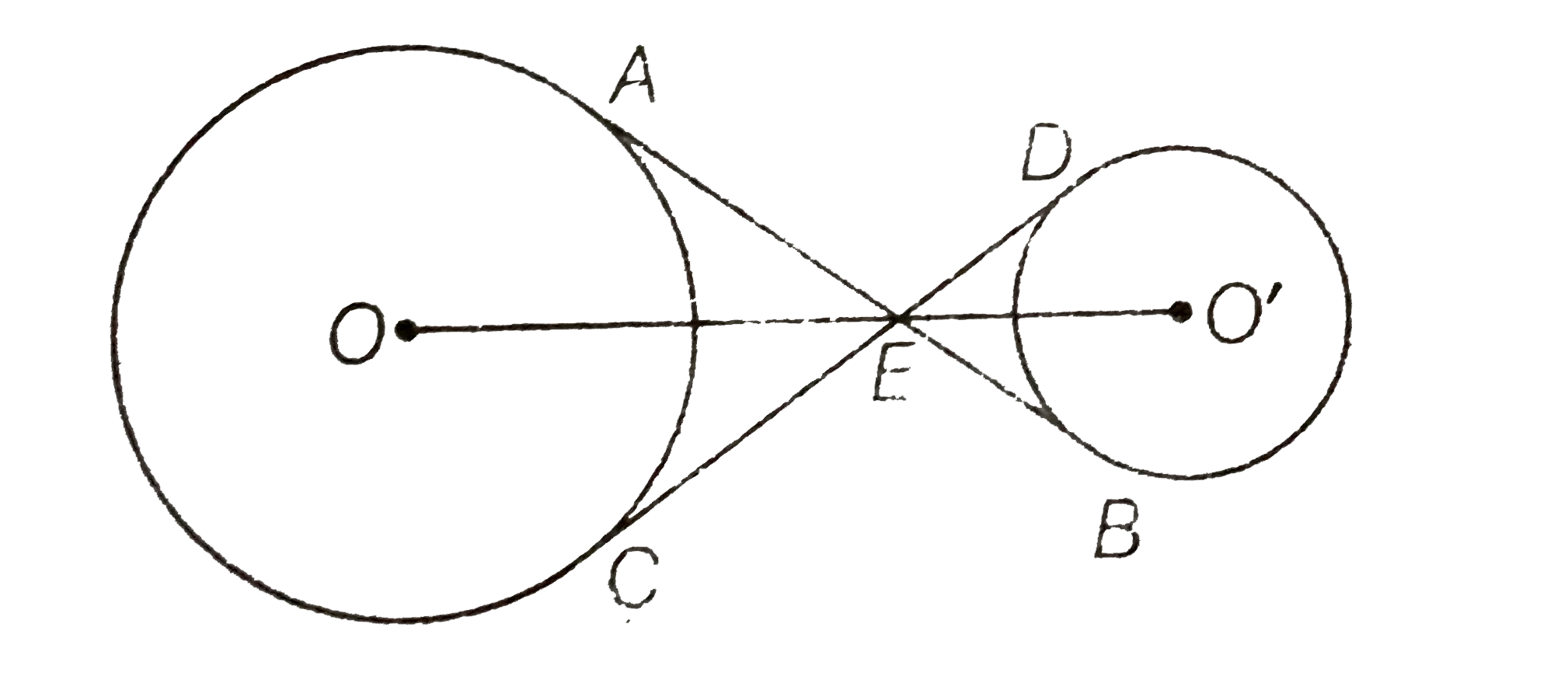
View SolutionIn a figure the common tangents, AB and CD to two circles with centers O and O' intersect at E. Prove that the points O, E and O' are collinear.
 View Solution
View SolutionIn figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB=CD
 View Solution
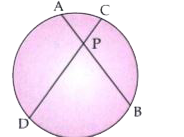
View SolutionAB and CD are two chords of a circle intersecting at P. Prove that AP×PB=CP×PD
 View Solution
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect point O. Prove that :
AB+BC+CD+DA<2(AC+BD)
 View Solution
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.
 View Solution
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionIn the figure, given below, straight lines AB and CD intersect at P, and AC//BD. Prove that :

ΔAPCandΔBPD are similar.View SolutionIn the given figure AC = BD, prove that AB = CD.
 View Solution
View Solution

