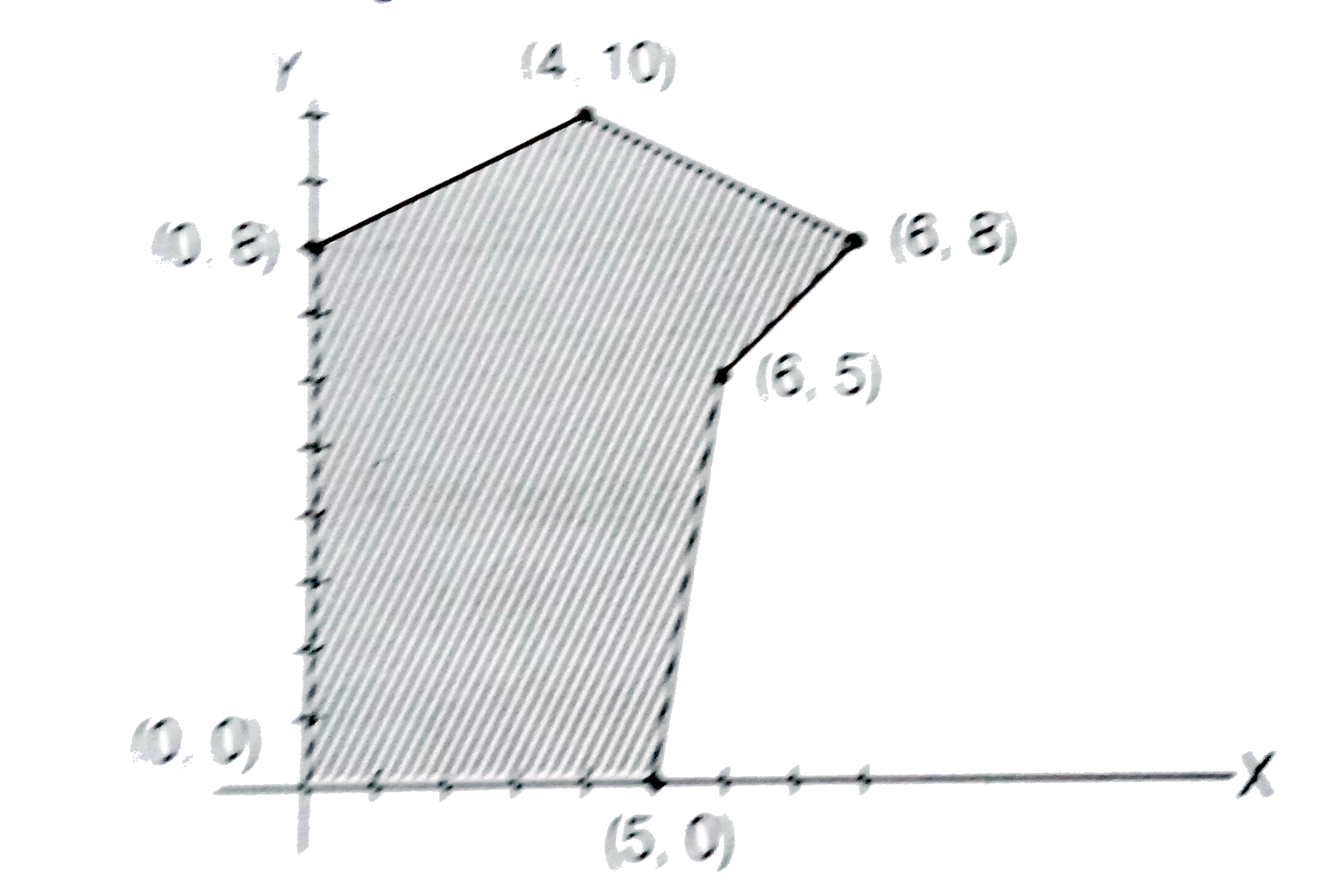
In the given graph,the feasible region for a LPP is shaded. The objective function Z=2x−3y,will be minimum at a) (4,10) b) (6,8) c) (0,8) d) (6,5)
Step by step video & image solution for In the given graph,the feasible region for a LPP is shaded. The objective function Z=2x-3y,will be minimum at a) (4,10) b) (6,8) c) (0,8) d) (6,5) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
If the corner points of the feasible region for an LPP are (0,2),(3,0),(6,0),(6,8),(0,5) then maximum of F - minimum of F =
A60B48C42D18 - Question 2 - Select One
The occurs point of the feasible region for an L.P.P. are (0, 3), (1, 1) and (3, 0). If objective function is Z=px+qy,p,q>0, then the condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is
Ap=2qBp=q2Cp=3qDp=q
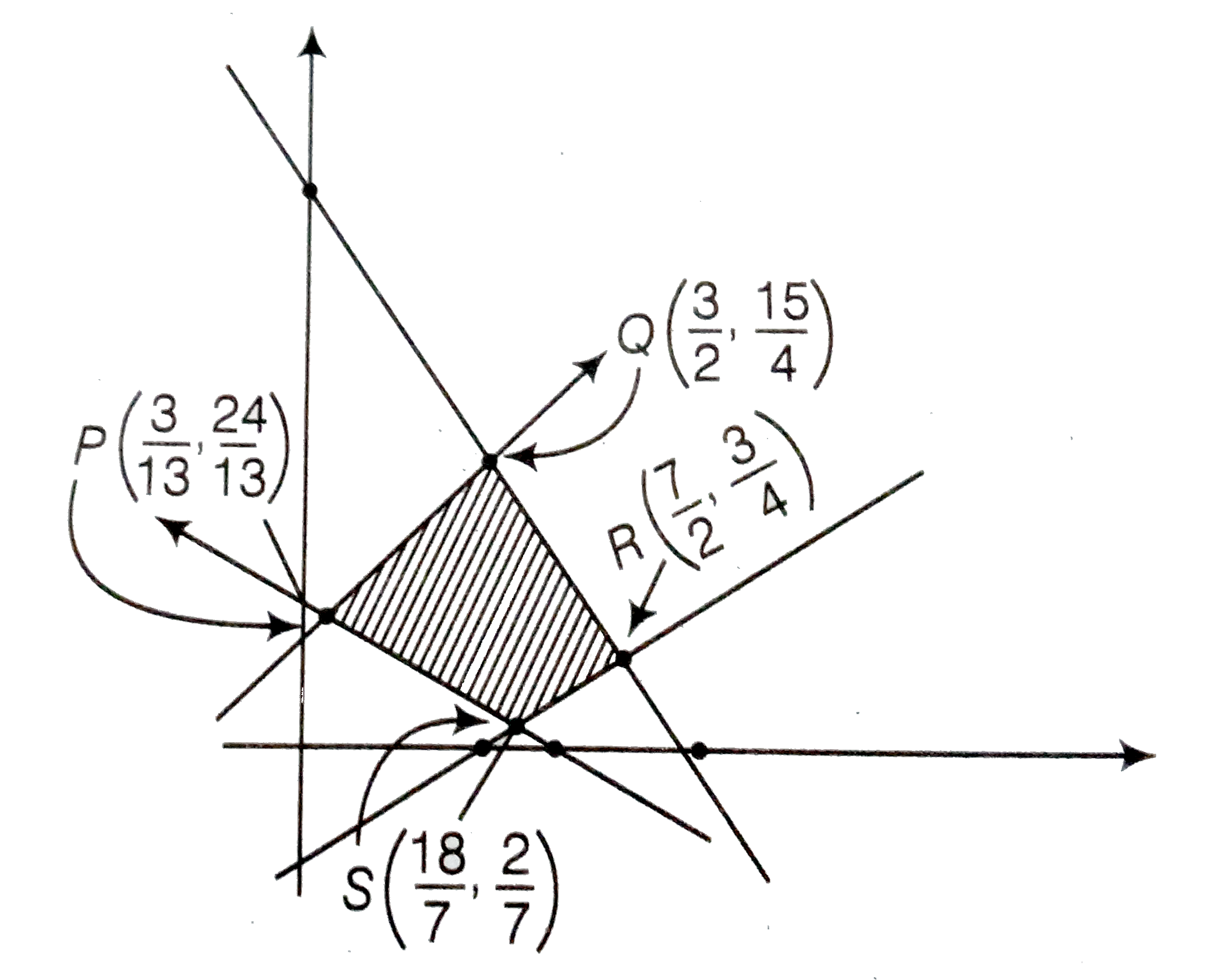
The feasible solution for a LPP is shown in following figure. Let Z=3x-4y be the objective function, Minimum of Z occurs at
 View Solution
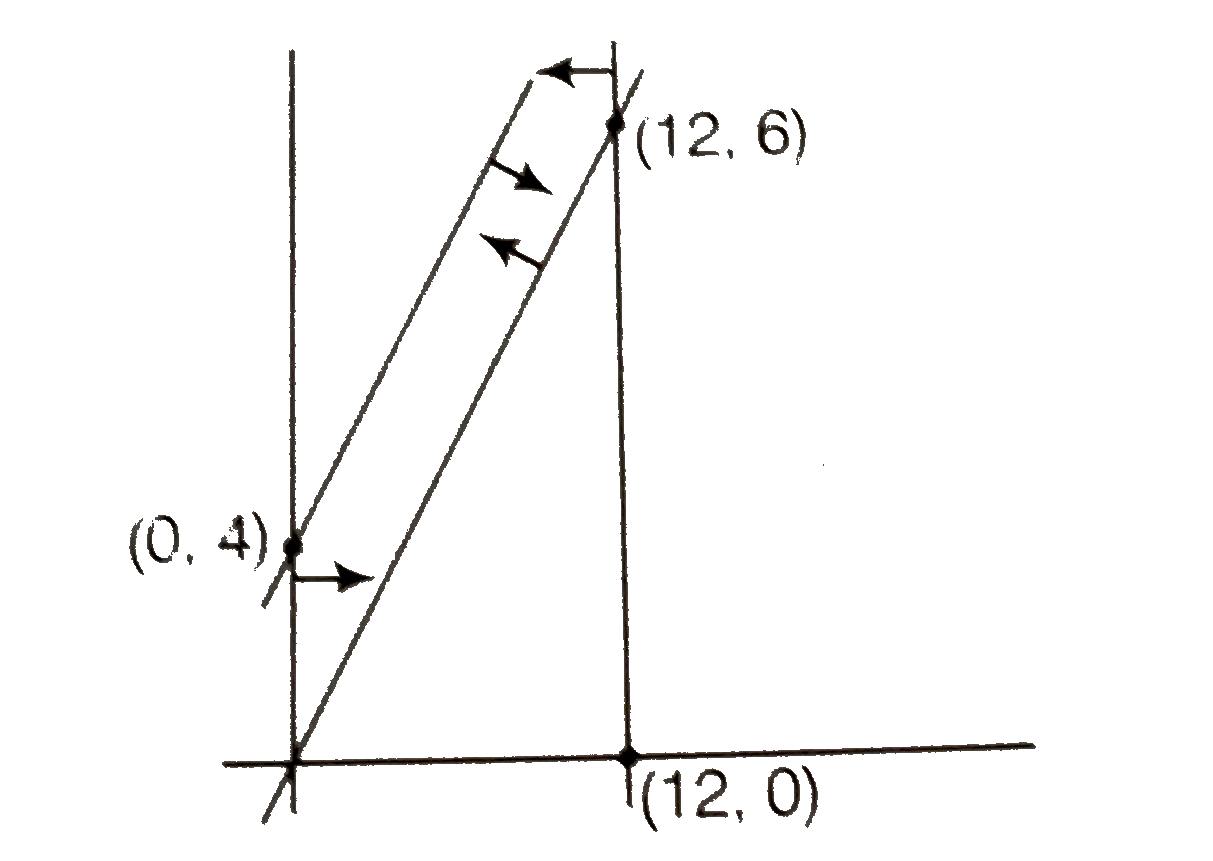
View SolutionThe feasible region for an LPP is shown in the following figure. Let F=3x−−4y be the objective function. Maximum value of F is
 View Solution
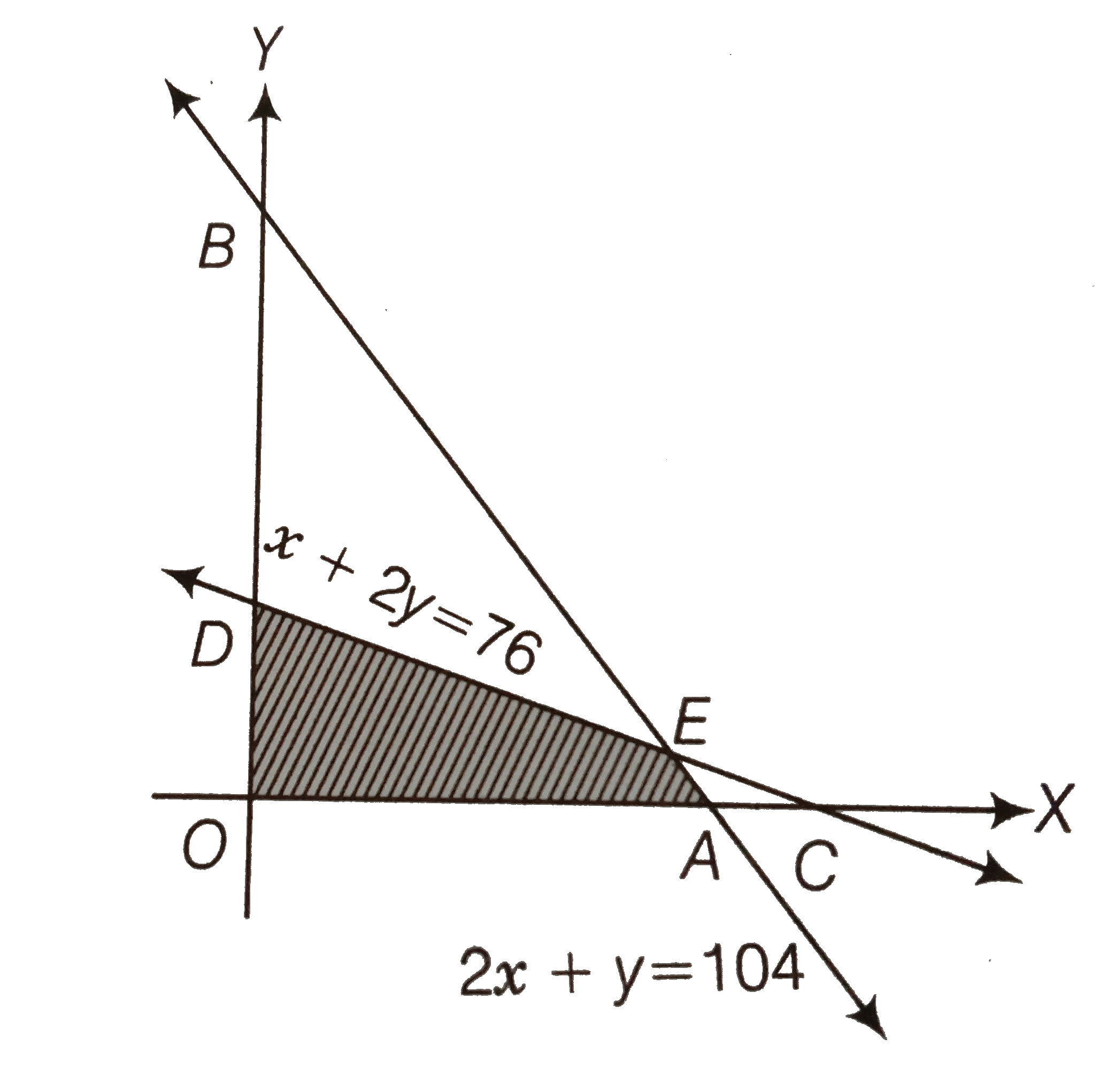
View SolutionFeasible region (shaded) for a LPP is shown in following figure. Maximise Z=5x+7y.
 View Solution
View SolutionDetermine the maximum value of Z=3x+4y, if the feasible reigon (shaded) for a LPP is shown in following figure
 View Solution
View SolutionCorner points of the feasible region for an LPP are ( 0,2) (3,0) ,(6,0),(6,8) and (0,5) Let Z=4 x + 6y be the objective function. The minimum value of F occurs at?
View SolutionCorner points of the feasible region for an LPP are (0,2),(3,0),(6,0),(6,8), and (0,5). Let F-4x+6y be the objective function. Determine the minimum valur of F occurs at
View Solution