In the feasible region for a LPP is ..., then the optimal value of the objective function Z= ax + by may or may not exist.
The correct Answer is:N/a
If the feasible region for a LPP is unbouded, then the optimal value of the objective fucnction Z=ax+by may or may not exist.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - TRUE/FALSE
2 Videos
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - OBJECTIVE
8 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Fillers
18 Videos
- MATRICESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example
101 Videos
Similar Questions
If the feasibile region for a LPP is unbounded, maximum or minimum of the objective function Z = ax + by may or may not exist.
View Solution
Z may not be:
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always finite.
View SolutionIn a LPP, the objective function is always.
View SolutionThe feasible region for an LPP is always a..polygon
View SolutionThe feasible region for an LPP is shown in the following figure. Let F=3x−−4y be the objective function. Maximum value of F is
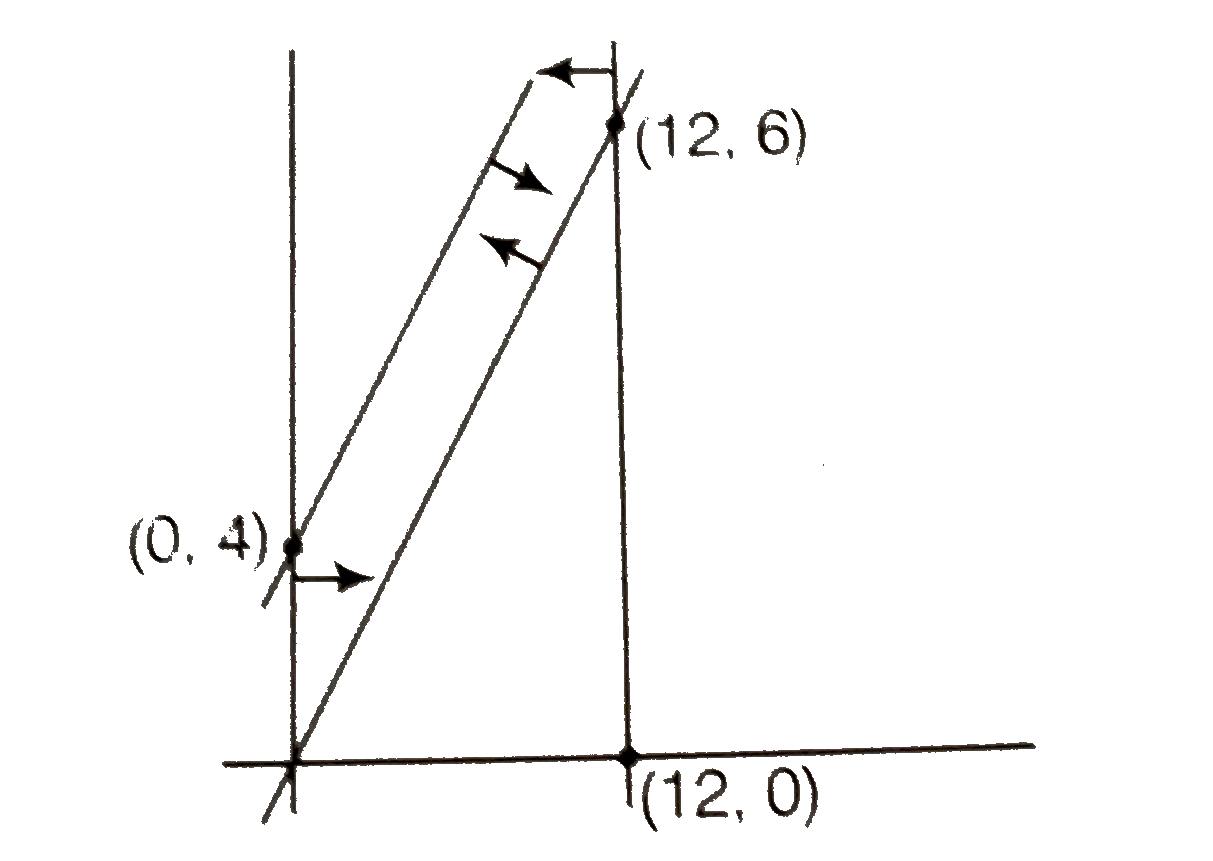
View SolutionIn the given graph,the feasible region for a LPP is shaded. The objective function Z=2x−3y,will be minimum at a) (4,10) b) (6,8) c) (0,8) d) (6,5)
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always 0, if origin is one of the corner point of the feasible region.
View SolutionThe feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.

View SolutionThe stem may function as :-
View Solution
