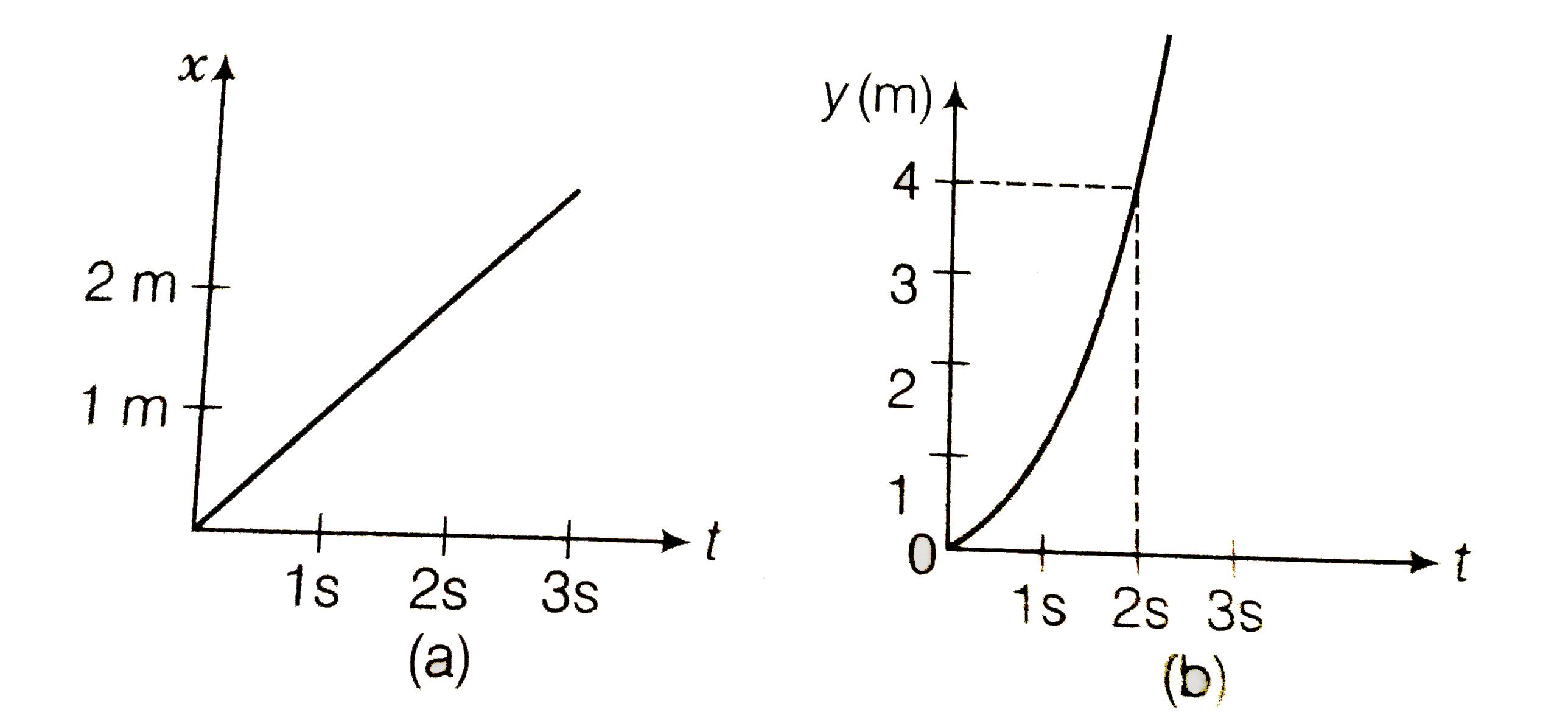
Figure shows (x,t) (y,t) diagram of a particle moving in 2-dimensions.
If the particle has a mass of 500 g , find the force (direction and magnitude) acting on the particle .
Clearly from diagram (a) , the variation can be related as
x = t ⇒dxdt=1 m/s
ax=0
From diagram (b) y=t2
⇒ dydt=2t or ay=d2ydt2=2m/s2
Hence , Iy=may=500×10−3×2=1N (∵m=500g)
Fx=max=0
Hence , net force , F=√F2x+F2y=Fy=1N (along y-axis)
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Long answer Type Questions9videos
LAWS OF MOTION
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Very short answer type Questions12videos
LAWS OF MOTION
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Multiple Choice Questions (MCQs)31videos
KINETIC THEORY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Long Answer Type Questions3videos
MECHANICAL PROPERTIES OF FLUIDS
Similar Questions
Knowledge Check
- Question 1 - Select One
The motion of a particle of mass m is described by y=ut+12gt2 . Find the force acting on the particale .
AmgBμtC2mgD2μt
The motion of a particle of mass m is described by y=ut+12gt2 . Find the force acting on the particale .
View SolutionThe velocity-time graph of a particle moving in a straight line is shown in figure. The mass of the particle is 2kg. Work done by all the forces acting on the particle in time interval between t=0 to t=10s is
 View Solution
View SolutionFigure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region
 View Solution
View SolutionThe fig. shows the v−t graph of a particle moving in straight line. Find the time when particle returns to the starting point.
 View Solution
View SolutionKinetic energy of a particle moving in a straight line is proportional to the time t. The magnitude of the force acting on the particle is :
View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.
 View Solution
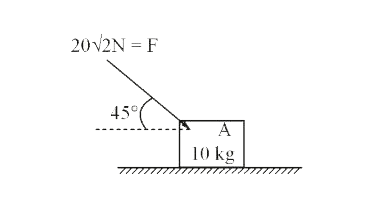
View SolutionA force F acts on a particle kept on a rough surface as shown in the figure. The particle is at rest. Find the net force applied by ground on the particle.
 View Solution
View Solution