Kinetic energy of a particle moving in a straight line is proportional to the time t. The magnitude of the force acting on the particle is :
Directly proportional to the speed of the particle
Directly proportional to √t
Inversely proportional to the speed of the particle
Inversely proportional to √t
The correct Answer is:C, D
To solve the problem, we need to analyze the relationship between kinetic energy, velocity, and force. Here’s a step-by-step breakdown:
Step 1: Understand the relationship between kinetic energy and time
Given that the kinetic energy (KE) of a particle is proportional to time t, we can express this as:
KE=ct
where c is a constant.
Step 2: Relate kinetic energy to velocity
The kinetic energy of a particle is also given by the formula:
KE=12mv2
where m is the mass of the particle and v is its velocity.
Step 3: Set the two expressions for kinetic energy equal
From the two expressions for kinetic energy, we can set them equal to each other:
12mv2=ct
Step 4: Solve for velocity
Rearranging the equation to solve for v2:
v2=2ctm
Taking the square root gives us:
v=√2cm√t
Let C0=√2cm, then:
v=C0√t
Step 5: Differentiate velocity to find acceleration
To find the acceleration a, we differentiate v with respect to time t:
a=dvdt=C0⋅12t−1/2=C02√t
Step 6: Relate acceleration to force
The force F acting on the particle is given by Newton's second law:
F=ma
Substituting the expression for acceleration:
F=m⋅C02√t=mC02√t
Step 7: Conclude the relationship of force with time
From the expression for force, we see that:
F∝1√t
This shows that the magnitude of the force acting on the particle is inversely proportional to the square root of time.
Final Answer
The magnitude of the force acting on the particle is inversely proportional to √t.
---
Given that the kinetic energy (KE) of a particle is proportional to time t, we can express this as:
KE=ct
where c is a constant.
The kinetic energy of a particle is also given by the formula:
KE=12mv2
where m is the mass of the particle and v is its velocity.
From the two expressions for kinetic energy, we can set them equal to each other:
12mv2=ct
Rearranging the equation to solve for v2:
v2=2ctm
Taking the square root gives us:
v=√2cm√t
Let C0=√2cm, then:
v=C0√t
To find the acceleration a, we differentiate v with respect to time t:
a=dvdt=C0⋅12t−1/2=C02√t
The force F acting on the particle is given by Newton's second law:
F=ma
Substituting the expression for acceleration:
F=m⋅C02√t=mC02√t
From the expression for force, we see that:
F∝1√t
This shows that the magnitude of the force acting on the particle is inversely proportional to the square root of time.
The magnitude of the force acting on the particle is inversely proportional to √t.
Topper's Solved these Questions
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:LEVEL - 2 PARAGRAPH QUESTIONS
Explore 2 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE MAIN (ARCHIVE)
Explore 53 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:Level - 1 PARAGRAPH QUESTIONS
Explore 3 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE Advanced (Archive)
Explore 89 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
Similar Questions
Kinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
View SolutionThe position of a particle moving on a straight line is proportional to the cube of the time elapsed. How does the acceleration of the particle depend on time elapsed?
View SolutionThe kinetic energy K of a particle moving along x - axis varies with its position (x) as shown in figure

The magnitude of force acting on particle at x = 9 mis
View SolutionIf the kinetic energy of a body is directly proportional to time t, the magnitude of the force acting on the body is
View SolutionThe displacement of a particle of mass 2kg moving in a straight line varies with times as x=(2t3+2)m. Impulse of the force acting on the particle over a time interval between t = 0 and t = 1 s is
View SolutionThe kinetic energy of a body moving along a straight line varies with time as shown in figure. The force acting on the body:

View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance s as K=as2. The force acting on the particle is
View SolutionIf average velocity of particle moving on a straight line is zero in a time interval, then
View SolutionThe fig. shows the displacement time graph of a particle moving on a straight line path. What is the magnitude of average velocity of the particle over 10 seconds?
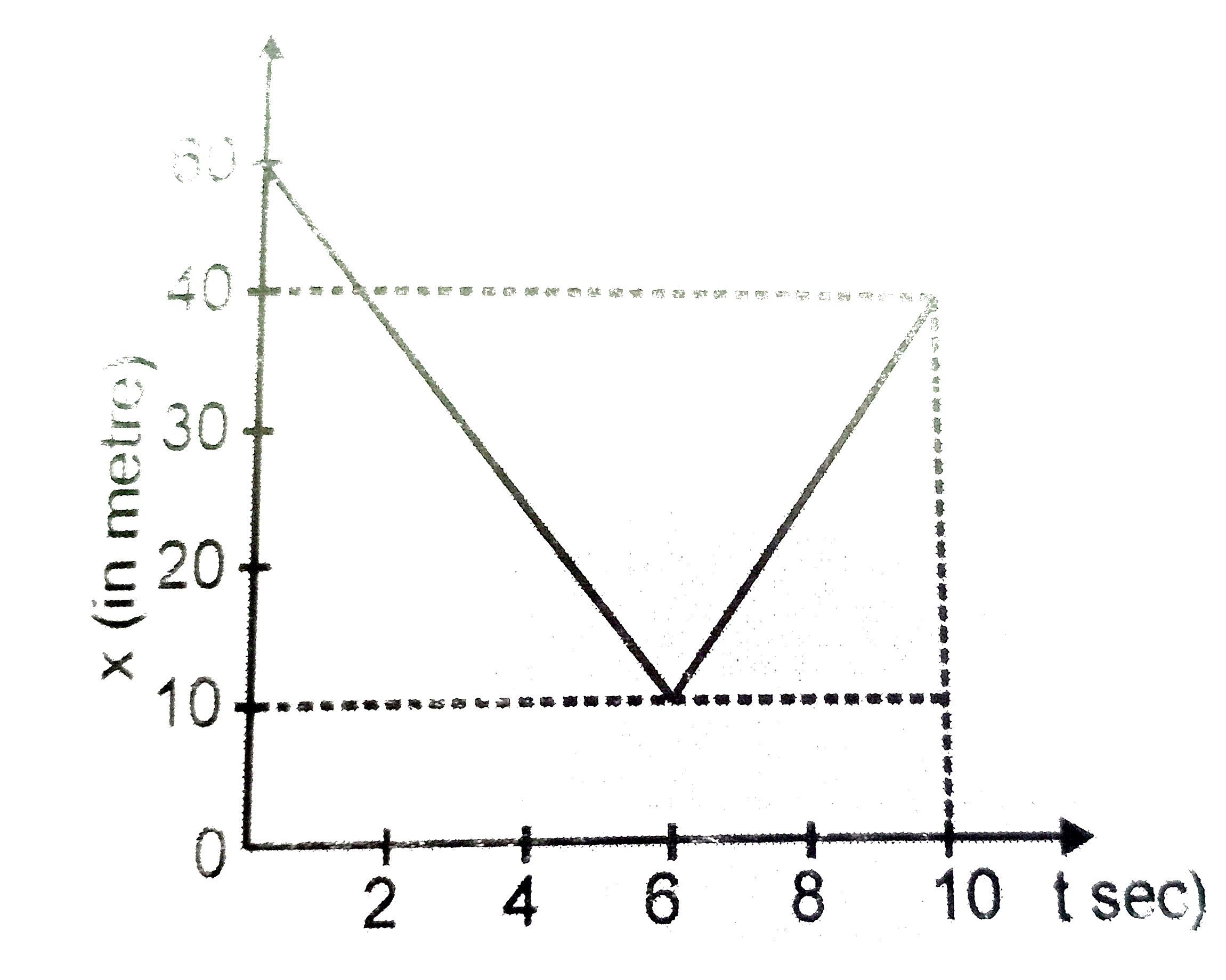
View SolutionDisplacement time graph of a particle moving in a straight line is a shown in figure.
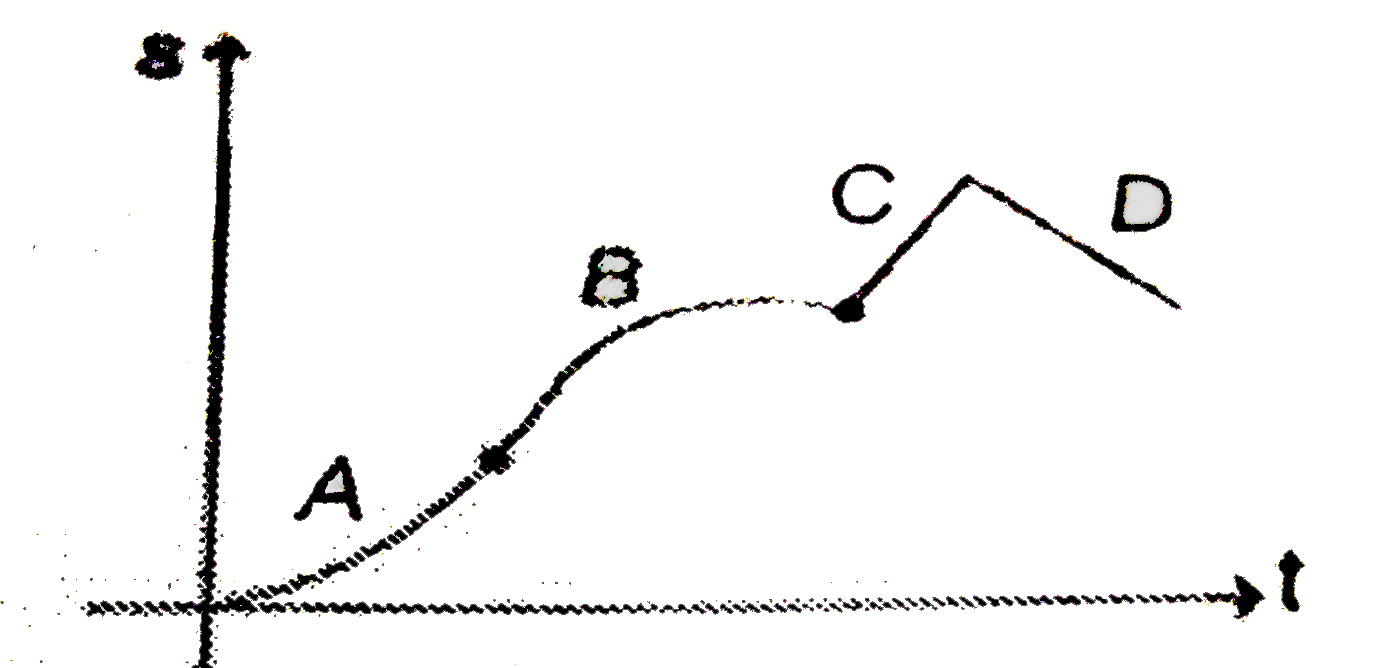
View Solution