Figure shows two identical particles 1 and 2 , each of mass m, ,moving in opposite r1andr2 are their respective position vectors drawn from point A which is the plane of the parallel lines, choose the correct options.
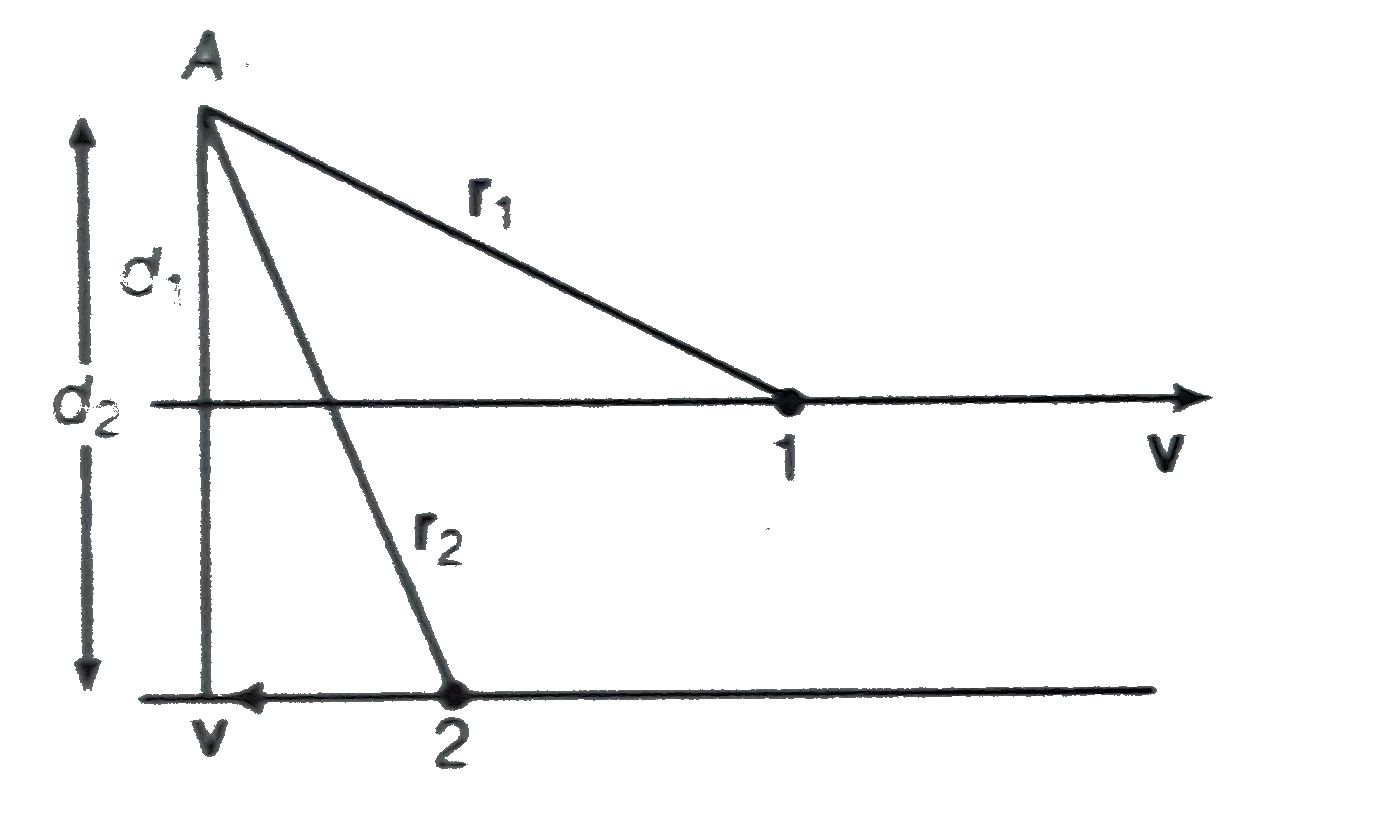
Agular momentum I1 of particle a about A is I=mv(d1)⊙
Angular momentum I2 of particle 2 about A is I2=mvr2⊙
total angular momentum of the system about A is I=mv(r1+r2)⊙
total angular momentum of the system about A is I=mv(d2−d1)⊗
The correct Answer is:a,b
the angular momentum L of a particle with respect toorigin is deined to be L=r×p where , r is the podsition vector of the particle and p is the linear momentum , The direction of L is is perpendicular to both d r and p by right hand rule .
For particle 1. I1=r1×mv is not of plane of the paper and perpendicular to r1 and p(mv) Similarly I2=r2×m(−v) is into the plane of the paper and perpendicular to r2and−p
Hence , total angular momentum
l=l1+l2=r1×mv+(−r2×mv)
|l|=mvd1−mvd2asd2>d1 total angular momentum will be inward
Hence I=mv(d2−d1)⊗
note : in the expression of angular momentum I=r×p the direction of l is taken by right hand rule .
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - very short answer type questions
18 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - Long answer type questions
12 Videos
- OSCILLATIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - OSCILLATIONSEXERCISE - All Questions
36 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Very short Answer type Questions
15 Videos
Similar Questions
Knowledge Check
Figure shows two identical particles 1 and 2, each of mass m, moving in opposite directions with same speed →V along parallel lines. At a particular instant, →r1 and →r2 are their respective position vectors drawn from point A which is in the plane of the parallel lines. Which of the following is the correct statement ?
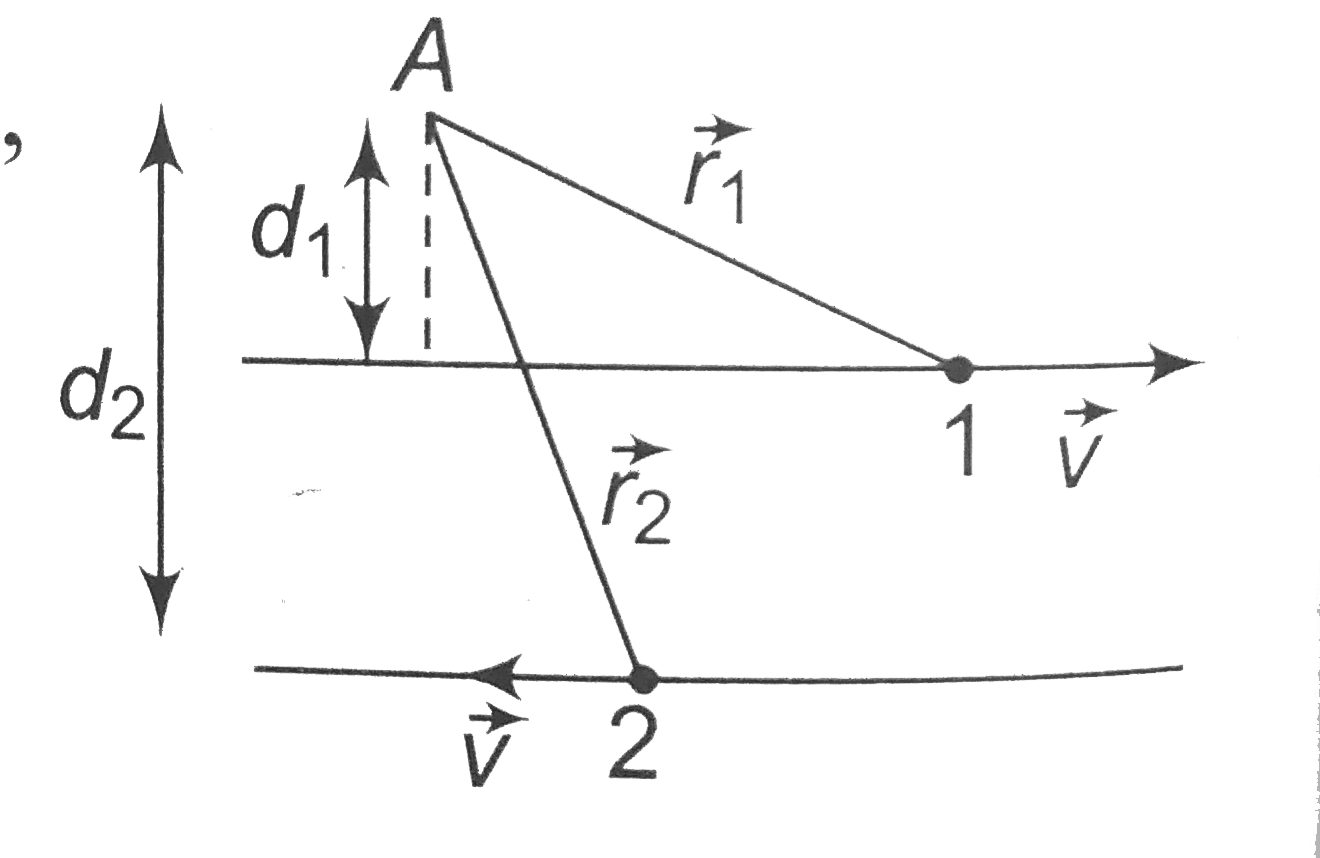 .AAngular momentum →L1 of particle 1 about A is →L1=mv→r1⊙BAngular momentum →L2 of particle 2 about A is →L2=mv→r2⊙CTotal angular momentum of the system about is →L=mv(→r1+→r2)⊙DTotal angular momentum of the system about A is →L=mv(d2−d1)⊗
.AAngular momentum →L1 of particle 1 about A is →L1=mv→r1⊙BAngular momentum →L2 of particle 2 about A is →L2=mv→r2⊙CTotal angular momentum of the system about is →L=mv(→r1+→r2)⊙DTotal angular momentum of the system about A is →L=mv(d2−d1)⊗
[Here, ⊗ represents a unit vector going into the page and ⊙ represents a unit vector coming out of the page].Figure shows two identical particles 1 and 2, each of mass m, moving in opposite directions with same speed →V along parallel lines. At a particular instant, →r1 and →r2 are their respective position vectors drawn from point A which is in the plane of the parallel lines. Which of the following is the correct statement ?
 .AAngular momentum →L1 of a particle 1 about A is →L1=mv→r1⊙BAngular momentum →L2 of particle 2 about A is →L2=mv→r2⊙CTotal angular momentum of the system about A is →L=mv(→r1+→r2)⊙DTotal angular momentum of the system about A is →L=mv(d2−d1)⊗
.AAngular momentum →L1 of a particle 1 about A is →L1=mv→r1⊙BAngular momentum →L2 of particle 2 about A is →L2=mv→r2⊙CTotal angular momentum of the system about A is →L=mv(→r1+→r2)⊙DTotal angular momentum of the system about A is →L=mv(d2−d1)⊗
⊗ represents a unit vector going into the page, ⊙ represent a unit vector coming out of the pageA particle of mass M is moving in a horizontal circle of radius R with uniform speed V. When it moves from one point to a diametrically opposite point , its
AKinetic energy changes by MV2/4Bmomentum does not changeCMomentum changes by 2MVDkinetic energy changes by MV2
Two batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
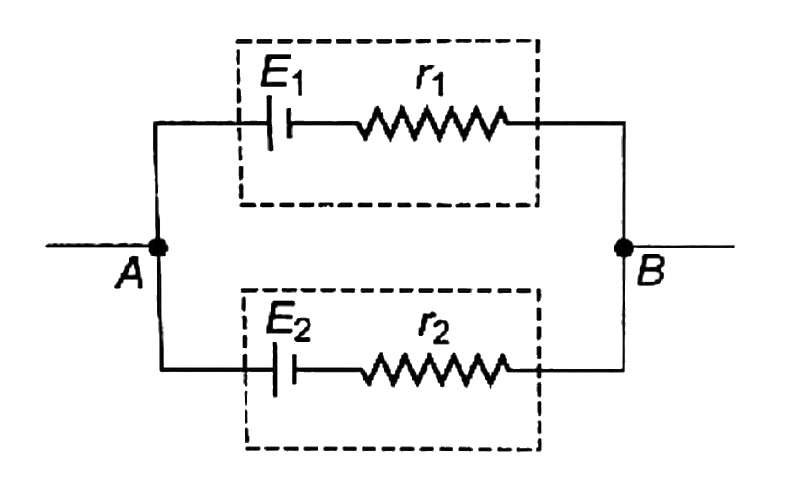
View SolutionTwo batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?

View SolutionThe figure represents two concentric shells of radii R1 and R2 and masses M1 and M2 respectively. The gravitational field intensity at the point A at distance a(R1<a<R2) is

View SolutionA particle of mass M is moving in a horizontal circle of radius R with uniform speed V. When it moves from one point to a diametrically opposite point, its
View SolutionTwo particles of masses m1andm2 are moving in concentric circle of radii r1andr2 such that their period are same. Then the ratio of their centripetal acceleration is
View Solution
