A disc of radius R is rotating with an angular $ω_{0}$ about a horizontal axis it is placed on a horizontal table . The coefficient of kinetic friction is $μ_{k}$
(a) what was the velocity of its centre of mass before being brought in contact with a the table ?
(B) what happens to the linear velocity of a point on its rim when placed in contact with the table ?
(c ) what happes to the linear speed of the centre of mass when disc is placed in contact with the table ?
(d) which force is responsible for the effects in (b) and (C ) ?
(e) wht condition should be sattisfied for rolling to begin ?
(f) Calculate the time taken for the rolling to begin .

Video Solution

Text Solution

Verified by Experts

(a) Before being Brought in contact with the the was in in pure rotational motion hence $v_{C M} = 0$

(b) when the disc is placed in contact with the table due to friction velocity of a point on the rim decreases ,
(c) when the rotating disc is placed in correct with the table due to friction centre of mass acquiries some linear velocity .
friction is responsible for the effects in (b) and ( c)
(e) when rolling starts $v_{C M} - ω R .$

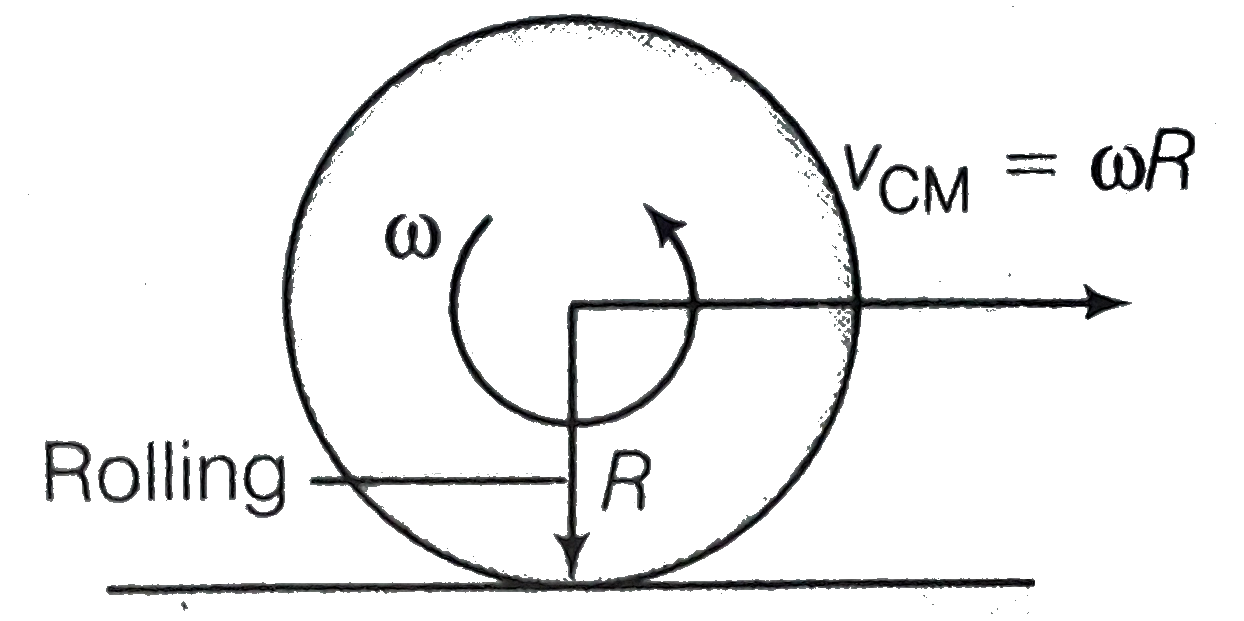
where $ω$ is angular speed of the disc when rolling just starts.
(f) Acceleration produced in centre of mass due to friction
$a_{C M} = \frac{F}{m} = \frac{μ_{k} m g}{m} = μ_{k} g .$

Angular retardation produced by the torque due to fricton .
$α = \frac{τ}{I} = \frac{μ_{k} m g R}{I} [∵ τ = (μ_{k} N) R = μ_{k} m g R]$
$∴ v_{C M = u_{C M}} + a_{C M^{t}}^{t}$
$\Rightarrow V_{C M} = μ_{k} gt (∵ U_{C M} = 0)$
$and ω = ω_{0} + a t$
$\Rightarrow ω = ω_{0} - \frac{μ_{k} m g R}{I} t$
For rolling without sliping , $\frac{V_{C M}}{R} = ω$
$\Rightarrow \frac{V_{C M}}{R} = ω_{0} - \frac{μ_{k} m g R}{I} t$
$\frac{μ_{k} g t}{R} = ω_{0} - \frac{μ_{k} m g R}{I} t$
$t = \frac{R ω_{0}}{μ_{k} g (1 + \frac{m R^{2}}{I})}$
note in this problem , frictional force help in seting pure rolloing motion .

Updated on:21/07/2023

A ring of radius $R$ is rotating with an angular speed $ω_{0}$ about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is $μ_{k}$ . The time after it starts rolling is.
A $\frac{ω_{o} μ_{k} R}{2} g$
B $\frac{ω_{o} g}{2} μ_{k} R$
C $\frac{2 ω_{o} R}{μ_{k}} g$
D $\frac{ω_{o} R}{2} μ_{k} g$