A unifrom disc of radius R , is resting on a table on its rim . The coeffficient of friction between disc and table Is μ (figure ) ,Now the disc is pulled with a force F as shown in the fiogure ,What is the maximum value of F for which the disc rolls without slipping ?

Consider the diagram below
Frictional force (f) is acting in the opposite direction of F
Let the acceeleration of centre of mass of disc be a then
F−F=Ma
where M is mass of the disc

the angular acceleration of the disc is
α=a/R(for pure rolling)
from τ=/α
⇒fR=(12MR2)α⇒fR=(12MR2)(aR)
⇒Ma=2F ....(ii)
from Eqs. (i) and (ii) we get
f=F/3[∵N=mg]
∵f≤μN=μmg
F3≤μMg⇒F≤3μMg
⇒Fmax=3μMg
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NCERT EXEMPLAR ENGLISHChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:very short answer type questions
Explore 18 Videos
- OSCILLATIONSBook:NCERT EXEMPLAR ENGLISHChapter:OSCILLATIONSExercise:All Questions
Explore 36 Videos
- THERMAL PROPERTIES OF MATTERBook:NCERT EXEMPLAR ENGLISHChapter:THERMAL PROPERTIES OF MATTERExercise:Very short Answer type Questions
Explore 15 Videos
Similar Questions
A unifrom disc of radius R, is resting on a table on its rim. The coefficient of friction between disc and table is μ Fig. Now the disc is spulled with a force F as shown in the Fig. What is the maximum value of F for which the disc rolls without slipping ?


View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View Solution
Knowledge Check
A unifrom disc of radius R, is resting on a table on its rim. The coefficient of friction between disc and table is μ Fig. Now the disc is pulled with a force F as shown in the Fig. What is the maximum value of F for which the disc rolls without slipping ?

 AμMgB2μMgC3μMgD4μMg
AμMgB2μMgC3μMgD4μMgA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank isAF2mB3F4mCF4mD3F2mA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Force of friction between the disc and the plank isAF2BF4CF3D2F3
A uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank is
View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Force of friction between the disc and the plank is
View SolutionA disc of radius R is pivoted at its rim. The period for small oscillations about an axis perpendicular to the plane of disc is
View SolutionA uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
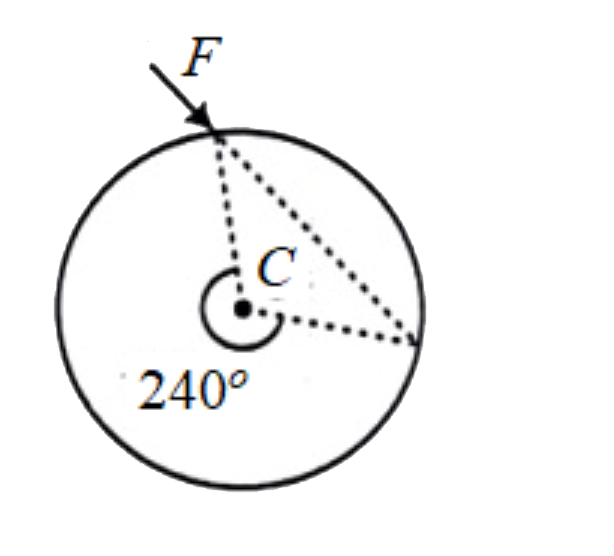
View Solution
