If Over a surface, then
The electric field inside the surface and on it is zero.
the electric field inside the surface is necessarily uniform
the number of flux lines entering the surface must be equal to the number of flux lines leaving it.
all charges must necessarily be outside the surface.
The correct Answer is:C, D
To solve the problem, we need to analyze the equation given and apply the principles of electric flux and Gauss's law.
1. Understanding the Equation:
We start with the integral given in the question:
∮SE⋅ds=0
This represents the electric flux (Φ) through a closed surface S.
2. Electric Flux Definition:
The electric flux through a surface is defined as:
Φ=∮SE⋅ds
If this integral equals zero, it indicates that the net electric field lines entering the surface are equal to the net electric field lines exiting the surface.
3. Applying Gauss's Law:
According to Gauss's law, the electric flux through a closed surface is related to the charge enclosed (Qenc) by the equation:
Φ=Qencϵ0
where ϵ0 is the permittivity of free space.
4. Setting the Flux to Zero:
Since we have established that Φ=0, we can set the equation from Gauss's law to zero:
Qencϵ0=0
This implies that:
Qenc=0
Therefore, there is no net charge enclosed within the surface.
5. Physical Interpretation:
The condition that the electric flux is zero means that the number of electric field lines entering the surface is equal to the number of electric field lines leaving the surface. This can occur when the surface is placed in a uniform electric field or when there are charges outside the surface that create an equal number of field lines entering and exiting.
6. Conclusion:
From the above analysis, we conclude that if ∮SE⋅ds=0, then:
- The charge enclosed within the surface is zero.
- The electric field lines entering the surface are equal to those exiting the surface.
Final Answer:
The correct options based on the analysis are:
- All charges must necessarily be outside the surface.
- The electric field inside the surface and on it is not necessarily zero, but the net flux is zero.
We start with the integral given in the question:
∮SE⋅ds=0
This represents the electric flux (Φ) through a closed surface S.
The electric flux through a surface is defined as:
Φ=∮SE⋅ds
If this integral equals zero, it indicates that the net electric field lines entering the surface are equal to the net electric field lines exiting the surface.
According to Gauss's law, the electric flux through a closed surface is related to the charge enclosed (Qenc) by the equation:
Φ=Qencϵ0
where ϵ0 is the permittivity of free space.
Since we have established that Φ=0, we can set the equation from Gauss's law to zero:
Qencϵ0=0
This implies that:
Qenc=0
Therefore, there is no net charge enclosed within the surface.
The condition that the electric flux is zero means that the number of electric field lines entering the surface is equal to the number of electric field lines leaving the surface. This can occur when the surface is placed in a uniform electric field or when there are charges outside the surface that create an equal number of field lines entering and exiting.
From the above analysis, we conclude that if ∮SE⋅ds=0, then:
- The charge enclosed within the surface is zero.
- The electric field lines entering the surface are equal to those exiting the surface.
The correct options based on the analysis are:
- All charges must necessarily be outside the surface.
- The electric field inside the surface and on it is not necessarily zero, but the net flux is zero.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDEXERCISE - Very short Type Question
6 Videos
- ELECTRIC CHARGES AND FIELDBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDEXERCISE - Short Answer Type question
6 Videos
- ELECTRIC CHARGES AND FIELDBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDEXERCISE - Long Answer Type Question
6 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - LONG ANSWER TYPE QUESTION
5 Videos
- ELECTROMAGNETIC INDUCTION BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - Long
11 Videos
Similar Questions
STATEMENT -1 : If ∮→E.¯¯¯¯ds over a closed surface is negative,it means the surface encloses a net negative charge.
STATEMENT-2 : We may have a Gaussian surface in which three lines enter and five field lines are coming out.
STATEMENT-3 : The quantity ∮→E.¯¯¯¯ds is independent of the charge distribution inside the surface.
View SolutionA plane EM wave travelling in vacuum along z-direction is given by E=E0 sin (kz−ωt)ˆi and B=B0 sin (kz−ωt)ˆj
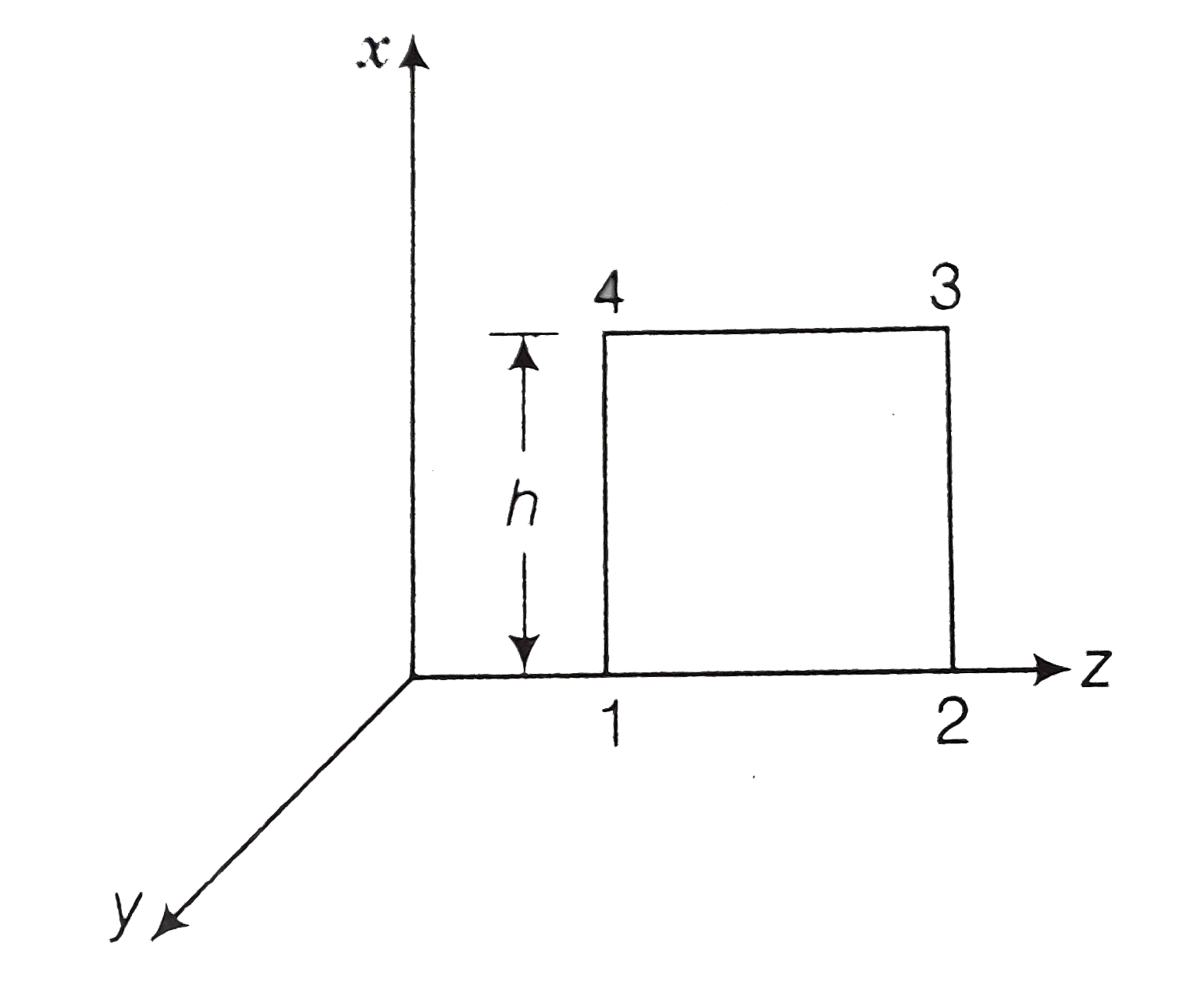
(i) Evaluate ∫E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate ∫B.ds over the surface bounded by loop 1234.
(iii) Use equation ∫E.dl=−dϕBdt to prove E0B0=c.
(iv) By using similar proces and the equation
∫B.dl=μ0I+ε0dϕEdt, prove that c1√μ0ε0
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
If the charge q3 and q4 are displaced (always remaining outside the Gaussian surface), then consider the following two statements :
A: Electric field at each point on the Gaussian surface will remain same .
B: The value of ∮→E.d→A for the Gaussian surface will remain same.
View Solution"It is easier to make a body roll over a surface than to slide". Why ?
View SolutionIf r is the radius, S the surface area and V the volume of a spherical bubble, prove that
(ii) dVdS∞r
View SolutionWhen transfer of pollen grains occurs over the surface of water , it is called
View SolutionIf V is the volume of a cuboid of dimensions a,b,candS is its surface area, then prove that SV=2(1a+1b+1c)
View SolutionIf for an Amperian loop ∮→B.→dl=0 does that mean →B=0 at every point on the Amperian loop ?
View SolutionA cylinder of radius R and length l is placed in a uniform electric field E parallel to the axis of the cylinder. The total flux over the curved surface of the cylinder is
View SolutionA block of mass 50 kg slides over a horizontal distance of 1m. If the coefficient of friction between their surface is 0.2, then work done against friction is (take g=9.8m/s2) :
View Solution
