A cylinder of radius R and length l is placed in a uniform electric field E parallel to the axis of the cylinder. The total flux over the curved surface of the cylinder is
zero
πR2E
2πR2E
E/πR2
The correct Answer is:A, B, C, D
To solve the problem of finding the total electric flux over the curved surface of a cylinder placed in a uniform electric field parallel to its axis, we can follow these steps:
1. Understand the Configuration:
- We have a cylinder with radius R and length l.
- The electric field →E is uniform and parallel to the axis of the cylinder.
2. Identify the Surface Area:
- The curved surface area of the cylinder can be calculated using the formula:
A=2πRl
- However, since we are interested in the flux through the curved surface, we will focus on the area vector direction.
3. Determine the Area Vector Direction:
- The area vector →A for the curved surface of the cylinder points radially outward, perpendicular to the surface.
- This means that the area vector is oriented perpendicular to the axis of the cylinder.
4. Evaluate the Dot Product:
- The electric flux Φ through a surface is given by:
Φ=→E⋅→A=∫→E⋅d→A
- Since the electric field →E is parallel to the axis of the cylinder and the area vector d→A for the curved surface is perpendicular to the electric field, we have:
→E⋅d→A=|→E||d→A|cos(90∘)=0
5. Conclusion:
- Since the dot product is zero, the total electric flux Φ through the curved surface of the cylinder is:
Φ=0
Final Answer:
The total flux over the curved surface of the cylinder is zero.
- We have a cylinder with radius R and length l.
- The electric field →E is uniform and parallel to the axis of the cylinder.
- The curved surface area of the cylinder can be calculated using the formula:
A=2πRl
- However, since we are interested in the flux through the curved surface, we will focus on the area vector direction.
- The area vector →A for the curved surface of the cylinder points radially outward, perpendicular to the surface.
- This means that the area vector is oriented perpendicular to the axis of the cylinder.
- The electric flux Φ through a surface is given by:
Φ=→E⋅→A=∫→E⋅d→A
- Since the electric field →E is parallel to the axis of the cylinder and the area vector d→A for the curved surface is perpendicular to the electric field, we have:
→E⋅d→A=|→E||d→A|cos(90∘)=0
- Since the dot product is zero, the total electric flux Φ through the curved surface of the cylinder is:
Φ=0
The total flux over the curved surface of the cylinder is zero.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Multiple Correct8videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Comprehension36videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - Subjective12videos
ELECTRIC FLUX AND GAUSS LAW
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.515videos
ELECTRIC POTENTIAL
Similar Questions
A cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View SolutionA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View SolutionConsider a cylindrical surface of radius R and length l in a uniform electric field E. Compute the electric flux if the axis of the cylinder is parallel to the field direction.
View SolutionA hollow half cylinder surface of radius R and length l is placed in a uniform electric field →E. Electric field is acting perpendicular on the plane ABCD. Find the flux through the curved surface of the hollow cylindrical surface
 View Solution
View SolutionA Gaussian surface in the cylinder of cross-section πa2 and length L is immersed in a uniform electric field E with the cylinder axis parallel to the field. The flux ϕ of the electric field through the closed surface is
View SolutionA cylindrical space of radius R is filled with a uniform magnetic induction parallel to the axis of the cylinder. If B charges at a constant rate, the graph showin the variation of induced electric field with distance r from the axis of cylinder is
 View Solution
View SolutionA insulating cylindrical rod of diameter d and length l(l>>d) has a uniform surface charge density such that the electric field just outside the curved surface of the cylinder at point M is E0. Find the electric field due to charge distribuition at point P(r>>l).
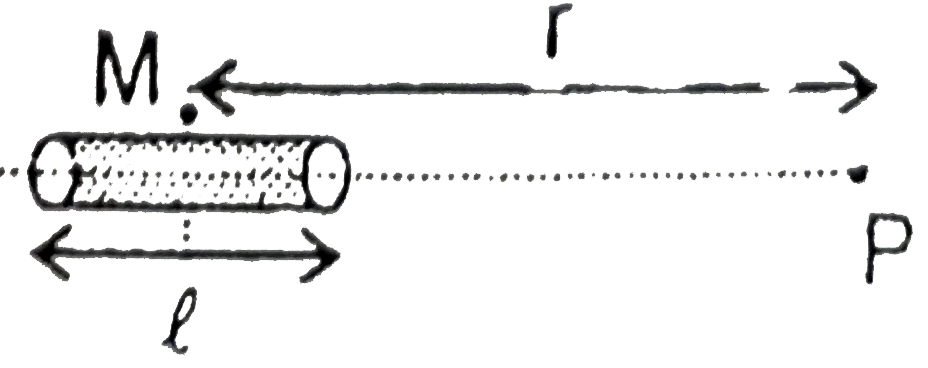 View Solution
View Solutiona hemispherical hollow body is placed in a uniform electric field E. the total flux linked with the curved surface is
 View Solution
View SolutionA hemispherical body of radius R is placed in a uniform electric field E. What is the flux linked with the curved surface if, the field is (a) parallel to the base, (b) perpendicular to the base.
View SolutionA hemispherical body of radius R is placed in a uniform electric field E. What is the flux linked with the curved surface if, the field is (a) parallel to the base, (b) perpendicular to the base.
View Solution

