Calculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
To calculate the potential on the axis of a ring due to a uniformly distributed charge Q along the ring of radius R, we can follow these steps:
Step 1: Understand the Setup
Consider a ring of radius R with a total charge Q uniformly distributed along its circumference. We want to find the electric potential V at a point P located on the axis of the ring at a distance z from the center of the ring.
Step 2: Differential Charge Element
Let’s denote a small element of charge on the ring as dq. The total charge Q is uniformly distributed, so the charge per unit length on the ring is given by:
λ=Q2πR
where λ is the linear charge density.
Step 3: Expression for Differential Potential
The electric potential dV at point P due to the small charge element dq is given by:
dV=kdqr
where k=14πϵ0 and r is the distance from the charge element dq to the point P.
Step 4: Calculate the Distance r
The distance r from the charge element dq to the point P can be expressed using the Pythagorean theorem:
r=√R2+z2
Step 5: Substitute dq
The differential charge dq can be expressed in terms of the linear charge density:
dq=λdl=Q2πRdl
where dl is the differential length along the ring.
Step 6: Integrate Over the Ring
The total potential V at point P is obtained by integrating dV around the entire ring:
V=∫dV=∫kdqr=∫kQ2πRdl√R2+z2
Since r is constant for all dq on the ring, we can factor it out of the integral:
V=kQ√R2+z2∫dl2πR
Step 7: Evaluate the Integral
The integral ∫dl over the entire circumference of the ring is simply 2πR:
∫dl=2πR
Thus, we have:
V=kQ√R2+z2⋅2πR2πR=kQ√R2+z2
Step 8: Final Expression for Potential
Substituting k=14πϵ0, we get:
V=Q4πϵ0√R2+z2
Summary
The potential V at a point on the axis of a ring with charge Q uniformly distributed along its circumference and radius R is given by:
V=Q4πϵ0√R2+z2
Consider a ring of radius R with a total charge Q uniformly distributed along its circumference. We want to find the electric potential V at a point P located on the axis of the ring at a distance z from the center of the ring.
Let’s denote a small element of charge on the ring as dq. The total charge Q is uniformly distributed, so the charge per unit length on the ring is given by:
λ=Q2πR
where λ is the linear charge density.
The electric potential dV at point P due to the small charge element dq is given by:
dV=kdqr
where k=14πϵ0 and r is the distance from the charge element dq to the point P.
The distance r from the charge element dq to the point P can be expressed using the Pythagorean theorem:
r=√R2+z2
The differential charge dq can be expressed in terms of the linear charge density:
dq=λdl=Q2πRdl
where dl is the differential length along the ring.
The total potential V at point P is obtained by integrating dV around the entire ring:
V=∫dV=∫kdqr=∫kQ2πRdl√R2+z2
Since r is constant for all dq on the ring, we can factor it out of the integral:
V=kQ√R2+z2∫dl2πR
The integral ∫dl over the entire circumference of the ring is simply 2πR:
∫dl=2πR
Thus, we have:
V=kQ√R2+z2⋅2πR2πR=kQ√R2+z2
Substituting k=14πϵ0, we get:
V=Q4πϵ0√R2+z2
The potential V at a point on the axis of a ring with charge Q uniformly distributed along its circumference and radius R is given by:
V=Q4πϵ0√R2+z2
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Long Answer Type Question
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - Very short type question
5 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - LONG ANSWER
5 Videos
- MAGNETISM AND MATTER BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - All Questions
24 Videos
Similar Questions
A short electric dipole is placed at a distance x from centre O on the axis of a ring of radius R and charge Q is uniformly distributed over tis.

The net force acting on the dipole will be
View SolutionCalculate electric field due to a charge uniformly distributed in a spherical volume
View SolutionIn a free space, a thin rod carrying uniformly distributed negative charge −q is placed symmetrically along the axis of a tin ring of radius R varrying uniformly dostributed charge Q. The mass of the rod is m and length is l=2R. The ring is fixed and the rod is free to move. The rod is displaced slightly along the axis of the ring and then released. Find the period T to the small amplitude oscillations of the rod.
View SolutionA thin glass rod is bent into a semicircle of radius r. A charge +Q is uniformly distributed along the upper half, and a charge -Q is uniformly distributed along the lower half, as shown in fig. The electric field E at P, the center of the semicircle, is

View SolutionA ring of radius R is placed in the plane its centre at origin and its axis along the x-asis and having uniformly distributed positive charge. A ring of radius r(<<R) and coaxial with the larger ring is moving along the axis with constant velcity , then the variation of electrical flux (ϕ) passing through the smaller ring with position will be best represent by :
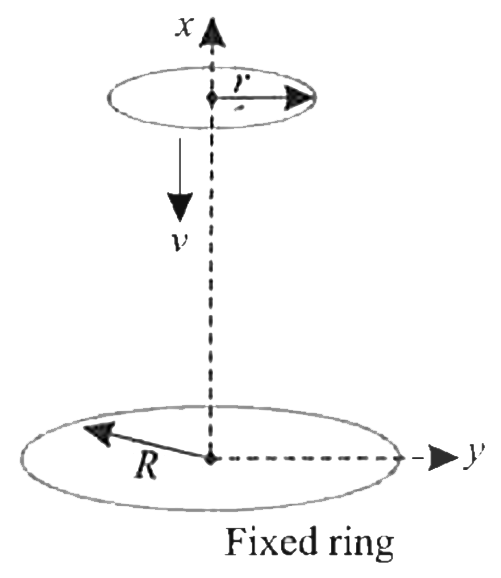
View SolutionBoth the ring and the conducting sphere are given the same charge Q. Determine the potential of the sphere. Assume that the centre of the sphere lies on the axis of th ring. Is it necessary that the charge on the ring be uniformly distributed to answer the above question ?
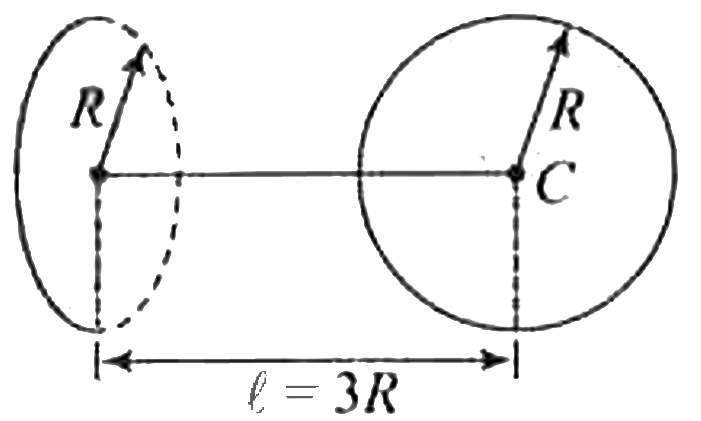
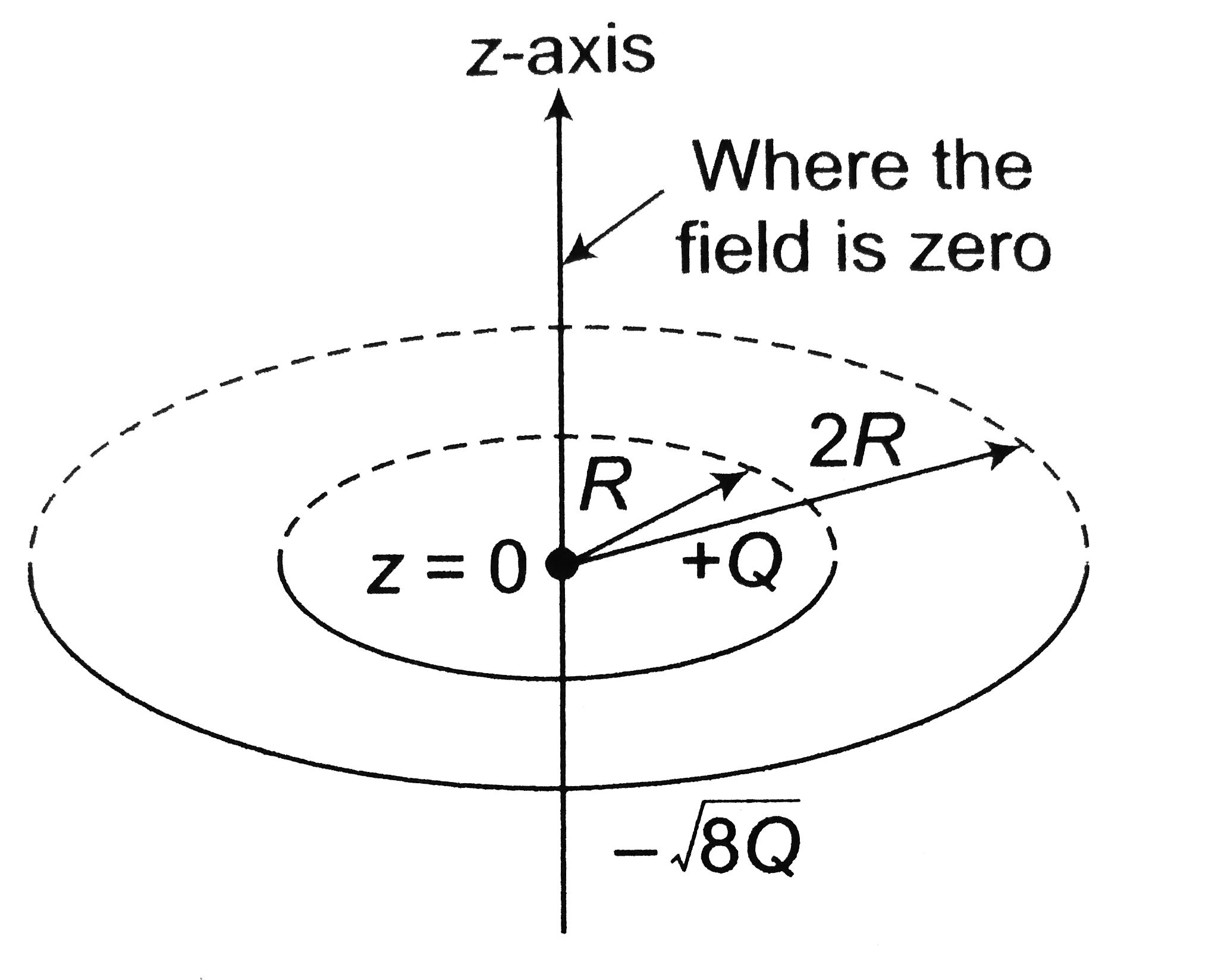
View SolutionTwo concentric rings, one of radius R and total charge +Q and second of radius 2R and total charge −√8Q, lie in x−y plane (i.e., z=0plane). The common centre of rings lies at origin and the common axis coincides with z-axis. The charge is uniformly distributed on both rings.
At what distance from origin is the net electric field on z-axis zero?
View SolutionSTATEMENT 1: When a negative charge -q is released at a distance R from the centre and along the axis of a uniformly and positvely charged fixed ring of radius R, the negative charge does oscillation but not SHM. STATEMENT 2: The force on negative charge is always towards the centre of the ring but it is not proportional to the displacement from the centre of the ring.
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionA charge is distributed uniformly over a ring of radius 'a'. Obtain an expression for the electric intensity E at a point on the axis of the ring . Hence show that for points at large distances from the ring it behaves like a point charge .
View Solution
