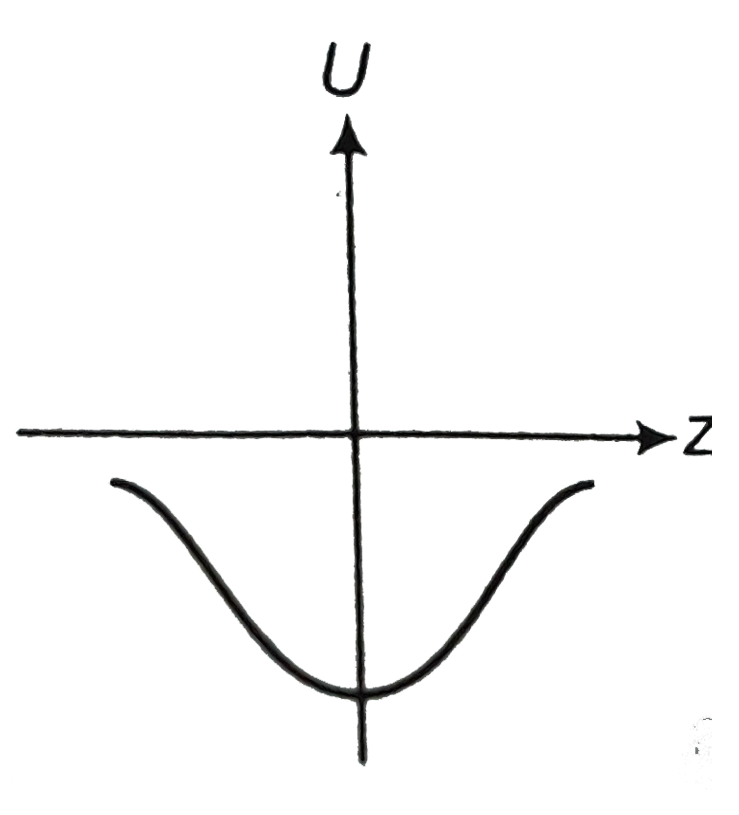
Calculate potential energy of a point charge $- q$ placed along the axis due to a charge $+ Q$ uniformly distributed along a ring of radius R. Sketch P.E. as a function of a axial distance z from the center of the ring, Looking at graph, can you see what happen if $- q$ is displaced slightly from the centre of the ring (along the axis) ?

Text Solution

Verified by Experts

let us take point P to be a t a distance x from the centre of the ring, as shown in figure. The charge element dq is a t a distance x from point P. therefore, V can be written as
$V = K_{e} \int \frac{d q}{r} = k_{e} \int \frac{d q}{\sqrt{z^{2} + a^{2}}}$
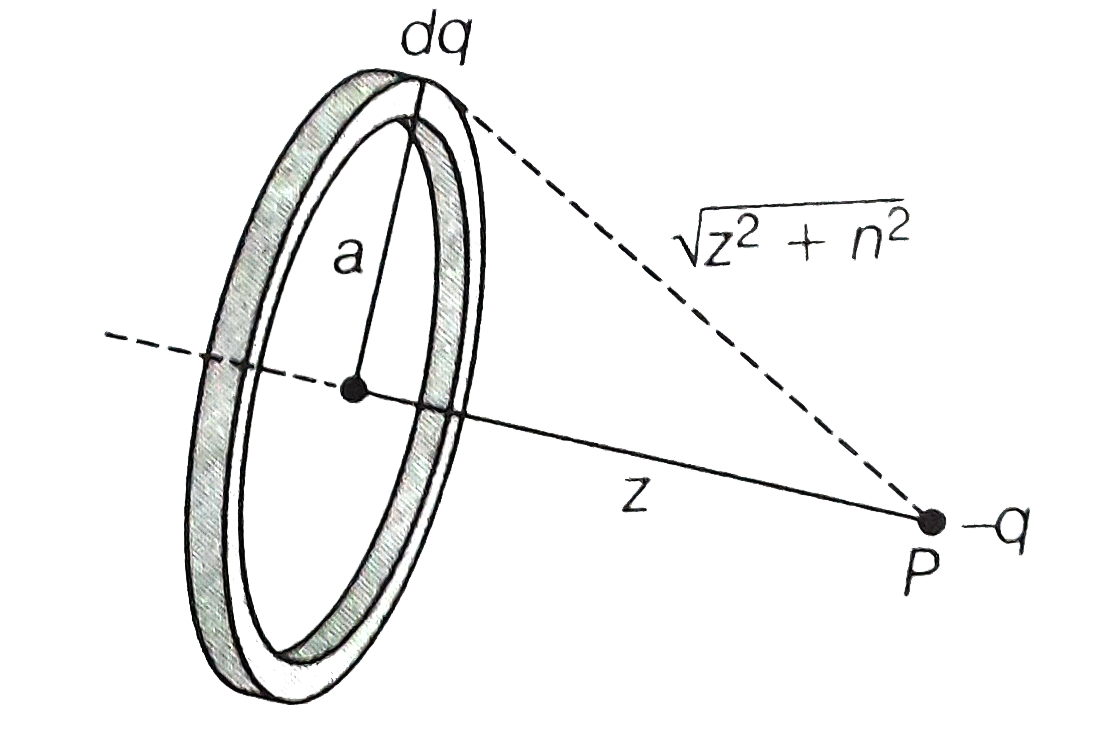ltBrgt Considering -q charge at P, the potential energy is given by
$U = W = q \times$ potential difference
$U = \frac{K_{e} Q (- q)}{\sqrt{z^{2} + a^{2}}}$
or $U = \frac{1}{4 π ε_{0}} \frac{- Q q}{\sqrt{z^{2} + a^{2}}}$
$= \frac{1}{4 π ε_{0} a} \frac{- Q q}{\sqrt{1 + {(\frac{z}{a})}^{2}}}$

This is the required expression.
The variation of potential energy with z is shown in the figure. the charge -q displaced would perrform oscillations.
Nothing can be concluded just by looking at the graph.

Updated on:21/07/2023

A positive charge $Q$ is uniformly distrubuted along a circular ring of radius $R$ .a small test chage $q$ is placed at the centre of the ring .The

Aif $q > 0$ and is displaced away from the centre in the plane of the ring.it will be pushed back towards the centre.
Bif $q < 0$ and is displaced away from the cnetre in the plane of the ring .it will never return to the centre and will continue moving till it hits the ring.
Cif $q < 0$ it will perform $S H M$ for small displacement along the axis
D $q$ at the centre of the ring is in an unstable equilibrium within the plane of the ring for $q < 0$
Charges $q$ is uniformly distributed over a thin half ring of radius $R$ . The electric field at the centre of the ring is
A $\frac{q}{2 π^{2} ε_{0} R^{2}}$
B $\frac{q}{4 π^{2} ε_{0} R^{2}}$
C $\frac{q}{4 π ε_{0} R^{2}}$
D $\frac{q}{2 π ε_{0} R^{2}}$