State the law of radioactive decay. Plot a graph showing the number (N) of undecayed nuclei as a function of time (t) for a given radioactive sample having half life T1/2
Depict in the plot the number of undecayed nuclei at
(i) t=3T1/2 and (ii) t=5T1/2.
Step-by-Step Solution
Step 1: State the Law of Radioactive Decay
The law of radioactive decay states that the rate of decay of a radioactive substance is directly proportional to the number of undecayed nuclei present at any given time. Mathematically, this can be expressed as:
dNdt=−λN
Where:
- N = number of undecayed nuclei at time t
- λ = decay constant
- t = time
The solution to this differential equation gives:
N(t)=N0e−λt
Where N0 is the initial number of undecayed nuclei at t=0.
Step 2: Relate Half-Life to Decay Constant
The half-life T1/2 is the time required for half of the radioactive nuclei to decay. It is related to the decay constant λ by the equation:
T1/2=ln(2)λ
From this, we can express λ as:
λ=ln(2)T1/2
Step 3: Calculate the Number of Undecayed Nuclei at Specific Times
Using the relationship between N and N0, we can find the number of undecayed nuclei at t=3T1/2 and t=5T1/2:
1. For t=3T1/2:
N(3T1/2)=N0e−λ(3T1/2)=N0e−3ln(2)=N0(12)3=N08
2. For t=5T1/2:
N(5T1/2)=N0e−λ(5T1/2)=N0e−5ln(2)=N0(12)5=N032
Step 4: Plot the Graph
To plot the graph of N versus t:
- The x-axis represents time t.
- The y-axis represents the number of undecayed nuclei N.
- Start with N0 at t=0.
- At t=T1/2, N=N02.
- At t=2T1/2, N=N04.
- At t=3T1/2, N=N08 (mark this point).
- At t=4T1/2, N=N016.
- At t=5T1/2, N=N032 (mark this point).
The graph will show an exponential decay curve, starting from N0 and approaching zero as time increases.
- N = number of undecayed nuclei at time t
- λ = decay constant
- t = time
- The y-axis represents the number of undecayed nuclei N.
- Start with N0 at t=0.
- At t=T1/2, N=N02.
- At t=2T1/2, N=N04.
- At t=3T1/2, N=N08 (mark this point).
- At t=4T1/2, N=N016.
- At t=5T1/2, N=N032 (mark this point).
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-II, DELHI BOARD
4 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-III, DELHI BOARD
4 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET -III
4 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
At time t=0 , number of nuclei of a radioactive substance are 100. At t=1 s these numbers become 90. Find the number of nuclei at t=2s.
View SolutionA radioactive sample undergoes decay as per the following gragp. At timet=0, the number of undecayed nuclei is N0. Calculate the number of nuclei left after 1h.
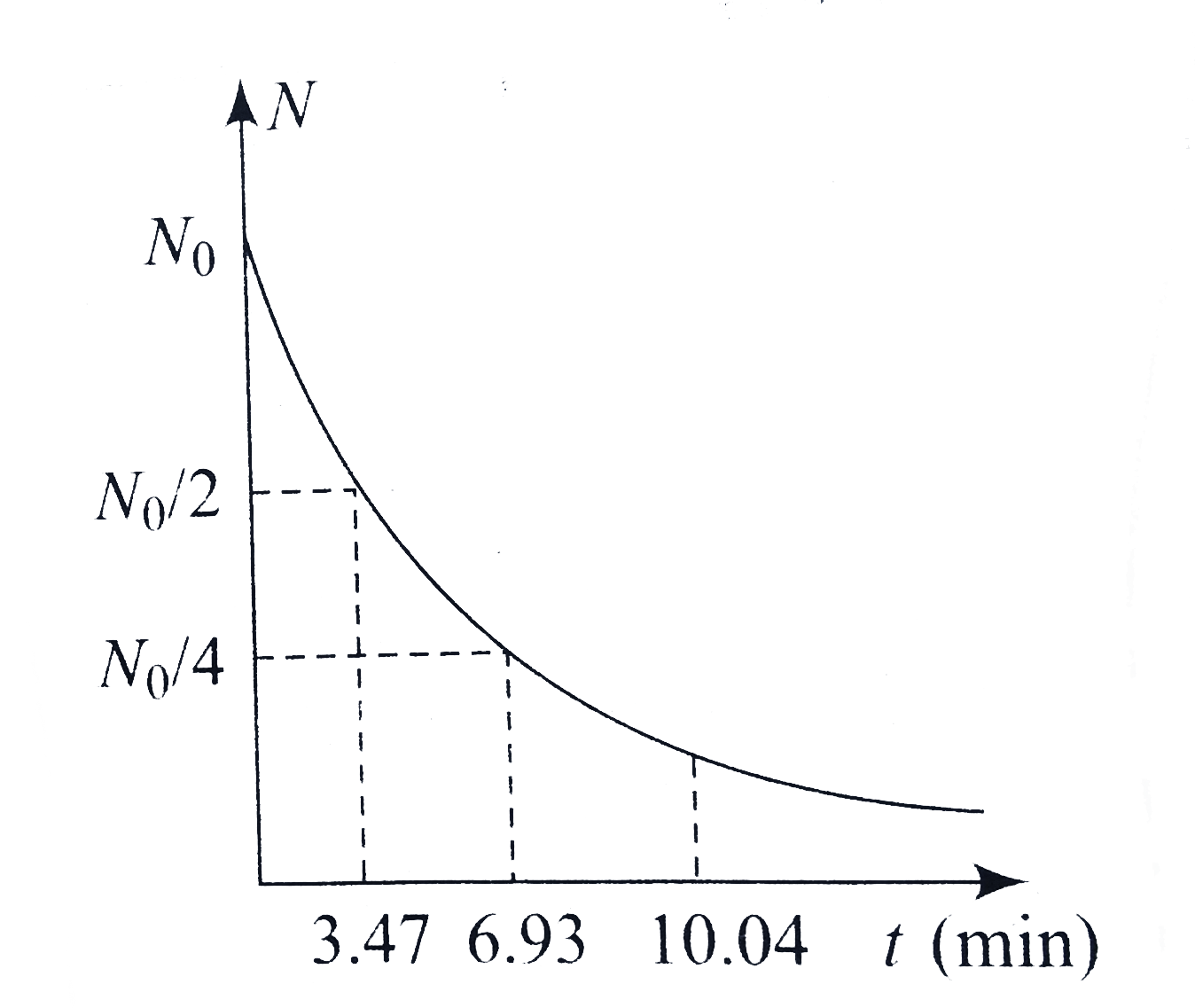 .
.
View Solution
Knowledge Check
At a given instant, there are 25% undecayed radioactive nuclei in a sample. After 10 seconds the number of undecayed nuclei reduces to 12.5%, the mean life of the nuclei is
A10.21 sB14.43 sC5.31 sD7.43 s
A radioactive sample undergoes decay as per the following gragp. At timet=0, the number of undecayed nuclei is N0. Calculate the number of nuclei left after 1h.
 .
.
View SolutionAt time t=0 , number of nuclei of a radioactive substance are 100. At t=1 s these numbers become 90. Find the number of nuclei at t=2s.
View SolutionA radioactive sample remains undecayed 916 after time t.How much sample remains undecayed after time t2
View SolutionFrom a radioactive substance n1 nuclei decay per second at an instant when total number of nuclei are n2. Find half-life of the radioactive substance.
View SolutionHalf-life of a radioactive substance is T. At time t_1 activity of a radioactive substance is R1 and at time t2 it is R2. Find the number of nuclei decayed in this interval of time.
View SolutionIn a sample of a radioactive substance, what fraction of the initial nuceli will remain undecayed after a time t=T/2 , where T=half -life of radioactive substance?
View SolutionAt t=0, number of radioactive nuclei of a radioactive substance are x and its radioactivity is y. Half-life of radioactive substance is T. Then,
View Solution