Plot a graph showing the variation of coulomb force (F) versus (1r2), where r is the distance between the two charges of each pair of charges:
(1μC,2μC)and(2μC−3μC). Interpet the graphs obtained.
To solve the problem of plotting the graph showing the variation of Coulomb force (F) versus 1r2 for the given pairs of charges, we will follow these steps:
Step 1: Understand Coulomb's Law
Coulomb's Law states that the force F between two point charges q1 and q2 separated by a distance r is given by:
F=14πϵ0q1q2r2
Where:
- F is the magnitude of the force between the charges,
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges,
- ϵ0 is the permittivity of free space.
Step 2: Identify the Charge Pairs
We have two pairs of charges:
1. Pair 1: q1=1μC and q2=2μC
2. Pair 2: q1=2μC and q2=−3μC
Step 3: Calculate the Force for Each Pair
Using Coulomb's Law, we can express the force for each pair as a function of 1r2.
For Pair 1 (1 µC and 2 µC):
F1=14πϵ0(1×10−6)(2×10−6)r2=2×10−124πϵ0r2
For Pair 2 (2 µC and -3 µC):
F2=14πϵ0(2×10−6)(−3×10−6)r2=−6×10−124πϵ0r2
Step 4: Plotting the Graph
1. X-axis: 1r2
2. Y-axis: F
- For Pair 1, the graph will show a positive slope, indicating a repulsive force.
- For Pair 2, the graph will show a negative slope, indicating an attractive force.
Step 5: Interpret the Graphs
- The graph for Pair 1 (1 µC and 2 µC) will be a straight line with a positive slope, indicating that as 1r2 increases, the repulsive force F also increases.
- The graph for Pair 2 (2 µC and -3 µC) will be a straight line with a negative slope, indicating that as 1r2 increases, the attractive force F becomes more negative (indicating stronger attraction).
Conclusion
The slope of the graph for the attractive force (Pair 2) is steeper than that for the repulsive force (Pair 1), indicating that the attractive force is greater in magnitude than the repulsive force for the same distance.
Coulomb's Law states that the force F between two point charges q1 and q2 separated by a distance r is given by:
F=14πϵ0q1q2r2
Where:
- F is the magnitude of the force between the charges,
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges,
- ϵ0 is the permittivity of free space.
We have two pairs of charges:
1. Pair 1: q1=1μC and q2=2μC
2. Pair 2: q1=2μC and q2=−3μC
Using Coulomb's Law, we can express the force for each pair as a function of 1r2.
F1=14πϵ0(1×10−6)(2×10−6)r2=2×10−124πϵ0r2
F2=14πϵ0(2×10−6)(−3×10−6)r2=−6×10−124πϵ0r2
1. X-axis: 1r2
2. Y-axis: F
- For Pair 2, the graph will show a negative slope, indicating an attractive force.
- The graph for Pair 1 (1 µC and 2 µC) will be a straight line with a positive slope, indicating that as 1r2 increases, the repulsive force F also increases.
- The graph for Pair 2 (2 µC and -3 µC) will be a straight line with a negative slope, indicating that as 1r2 increases, the attractive force F becomes more negative (indicating stronger attraction).
The slope of the graph for the attractive force (Pair 2) is steeper than that for the repulsive force (Pair 1), indicating that the attractive force is greater in magnitude than the repulsive force for the same distance.
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set- II]4videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - [Set-III]3videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SET-III, DELHI BOARD4videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
The graph shows the variation of lnRv/s1T2, where R is resistance and T is temperature. Then find R as function T.
_2019_CBT5_E01_037_Q01.png) View Solution
View SolutionPlot a graph showing variation of de-broglie wavelength λ versus 1/√V, where V is accelerating potential for two particle A and P carrying same charge but of masses m1andm2(m1>m2). Which one of the two represents a particle of smaller mass and why?
View SolutionThe force between two similar charges of magnitude 2C each separated by a distance 2km
View SolutionThe distance between the two charges 25μC and 36μC is 11cm. At what point on the line joining the two, the intensity will be zero
View SolutionFind the charge on the four capacirtors of capacitances 1(mu)F,2(mu)F,3(mu)F,and 4(mu)F, shown in figure.
 View Solution
View SolutionThe force of attractions between two charges 8μC and −4μC is 0.2 N. Find the distance of separation.
View SolutionThe force between two charges separated by a distance 1m is 1.8N. The charges are in the ratio 1:2 then the charges are
View SolutionWhich of the following graphs represents the relationship between the force F between two point charges and the distance r between them :
View SolutionIn the figure shown. Find the e.m.f. ɛ for which charge on 2μF capacitor is 4μC.
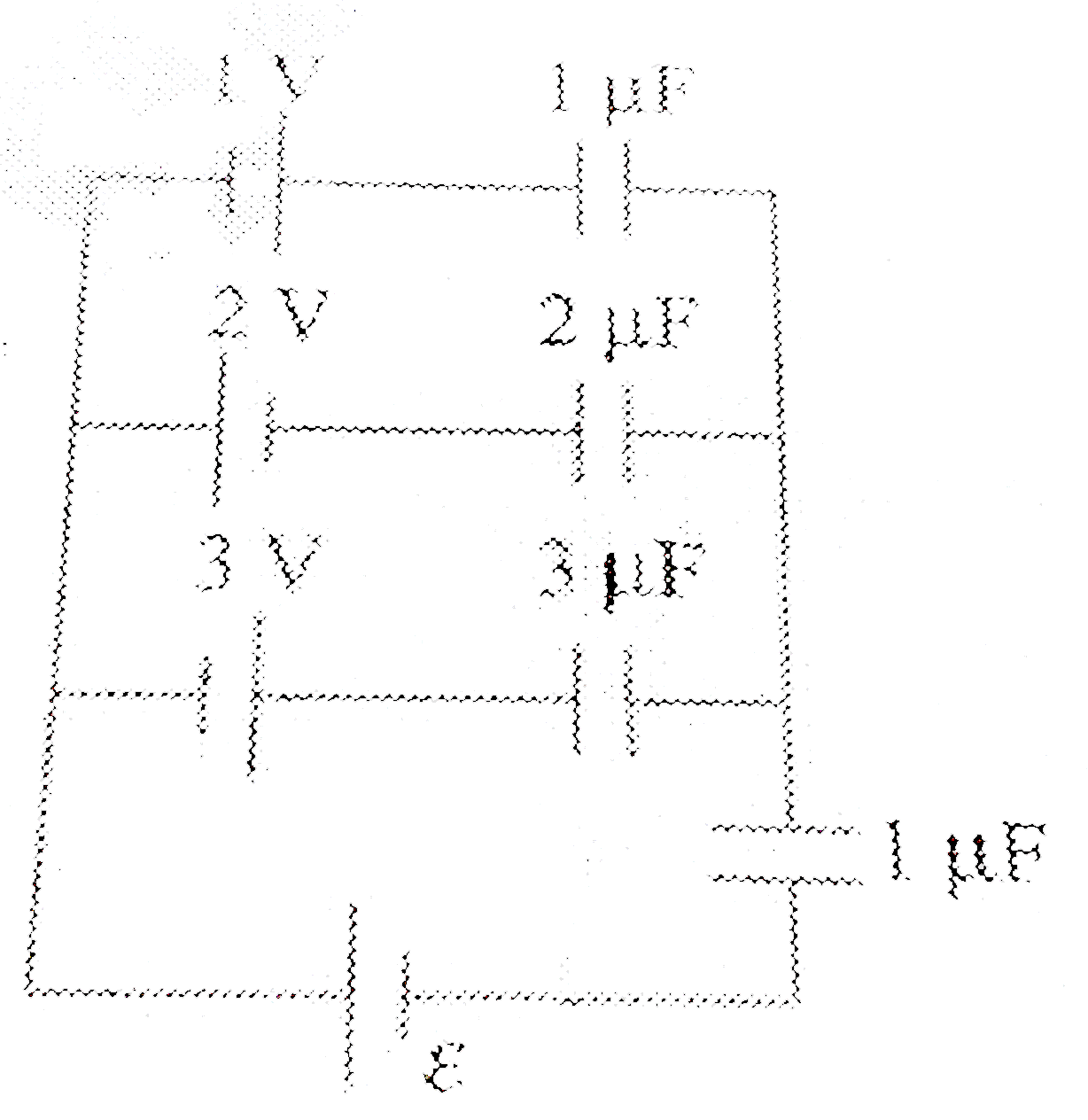 View Solution
View SolutionTwo point charges of 20μC and 80μC are 10 cm apart where will the electric field strength be zero on the line joining the charges from 20μC charge
View Solution

