C1=20μF,C2=30μFandC3=15μF are connected in series and the insulated plate of C1 is at a potential of 90 V, one plate of C3 being earthed. What is the potential difference between the plates of C2 ?
To solve the problem, we will follow these steps:
Step 1: Calculate the Equivalent Capacitance
The three capacitors C1, C2, and C3 are connected in series. The formula for the equivalent capacitance C of capacitors in series is given by:
1C=1C1+1C2+1C3
Substituting the values:
C1=20μF=20×10−6F
C2=30μF=30×10−6F
C3=15μF=15×10−6F
Thus,
1C=120×10−6+130×10−6+115×10−6
Calculating each term:
1C=120+130+115
Finding a common denominator (which is 60):
1C=360+260+460=960=320
Now, taking the reciprocal to find C:
C=203μF=203×10−6F
Step 2: Calculate the Charge on the Capacitors
The total voltage V applied across the series combination is 90 V. The charge Q on the capacitors can be calculated using the formula:
Q=C⋅V
Substituting the values:
Q=(203×10−6)×90
Calculating Q:
Q=20×903×10−6=600×10−6C
Step 3: Calculate the Potential Difference Across C2
The potential difference V2 across capacitor C2 can be calculated using the formula:
V2=QC2
Substituting the values:
V2=600×10−630×10−6
Calculating V2:
V2=60030=20V
Conclusion
The potential difference between the plates of C2 is 20 V.
---
The three capacitors C1, C2, and C3 are connected in series. The formula for the equivalent capacitance C of capacitors in series is given by:
C2=30μF=30×10−6F
C3=15μF=15×10−6F
The total voltage V applied across the series combination is 90 V. The charge Q on the capacitors can be calculated using the formula:
The potential difference V2 across capacitor C2 can be calculated using the formula:
The potential difference between the plates of C2 is 20 V.
Similar Questions
The force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionThree capacitors of 2μF,3μF and 6μF are joined in series and the combination is charged by means of a 24 volt battery. The potential difference between the plates of the 6μF capacitor is
View SolutionTwo capacitors of capacitances C1=2μF and C2=8μF are connected in series and the resulting combination is connected across a 300V battery. Calculate the charge, potential difference and energy stored in the capacitor separately.
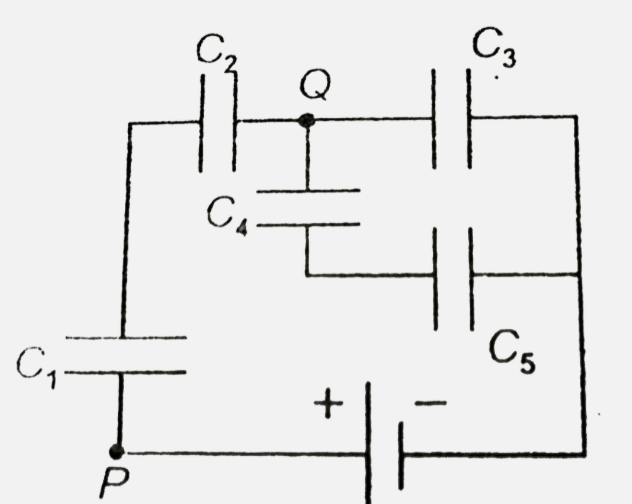
View SolutionIn the circuit shown C1=15μF,C2==30μF,C3=30μF,C4=30μF and C5=60μF. At steady state, the potential difference between points P and Q is 50 V. Calculate the potential difference across capacitor with capacitance C5
View SolutionIn a parallel plate capacitor of capacitor 1μF two plates are given charges 2μC and 4μC the potential difference between the plates of the capacitor is
_2019_CBT2_E01_002_Q01.png)
View SolutionThree capacitors 3μF,6μF and 6μF are connected in series to source of 120 V. The potential difference in volt, across the 3μF capacitor will be
View SolutionIn, given C1=3μF,C2=5μF,C3=9μF, and C4=13μF. What is the potential differnce between points A and B?
 .
.
View SolutionThree capacitors C1=3μF,C2=6μFandC3=10μF are connected to a 50 V battery as shown in the figure below:
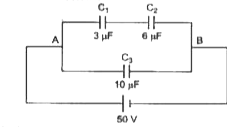
Calculate :
The charge on C1
View SolutionA charge of 1μC is given to one plate of a parallel - plate capacitor of capacitance 0.1μF and a charge of 2μC is given to the other plate . Find the potential difference developed between the plate .
View SolutionOne plate of a capacitor of capacitance 2μF has total charge +10μC and its other plate has total charge +40μC. The potential difference between the plates is (in Volt).
View Solution
