In a series LR circuit and power factor of the circuit is . When capacitor which capacitance C such that is put in series , the power factor becomes .Calculate
To solve the problem, we will follow these steps:
Step 1: Understand the Power Factor in the LR Circuit
In a series LR circuit, the power factor P1 is given by the formula:
P1=cosϕ1=RZ
where Z is the impedance of the circuit.
Step 2: Calculate the Impedance in the LR Circuit
The impedance Z in an LR circuit is given by:
Z=√R2+X2L
Given that XL=R, we can substitute this into the impedance formula:
Z=√R2+R2=√2R2=R√2
Step 3: Calculate the Power Factor P1
Now substituting Z back into the power factor formula:
P1=RR√2=1√2
Step 4: Introduce the Capacitor
When a capacitor is added such that XL=XC, the new power factor P2 is calculated. The capacitive reactance XC is given by:
XC=1ωC
Since XL=XC, we have XL−XC=0.
Step 5: Calculate the New Impedance Z with the Capacitor
The new impedance Z when the capacitor is added is:
Z=√R2+(XL−XC)2=√R2+02=R
Step 6: Calculate the Power Factor P2
Now substituting Z into the power factor formula:
P2=RR=1
Step 7: Calculate the Ratio P1P2
Finally, we can find the ratio of the power factors:
P1P2=1√21=1√2
Final Answer
P1P2=1√2
---
In a series LR circuit, the power factor P1 is given by the formula:
P1=cosϕ1=RZ
where Z is the impedance of the circuit.
The impedance Z in an LR circuit is given by:
Z=√R2+X2L
Given that XL=R, we can substitute this into the impedance formula:
Z=√R2+R2=√2R2=R√2
Now substituting Z back into the power factor formula:
P1=RR√2=1√2
When a capacitor is added such that XL=XC, the new power factor P2 is calculated. The capacitive reactance XC is given by:
XC=1ωC
Since XL=XC, we have XL−XC=0.
The new impedance Z when the capacitor is added is:
Z=√R2+(XL−XC)2=√R2+02=R
Now substituting Z into the power factor formula:
P2=RR=1
Finally, we can find the ratio of the power factors:
P1P2=1√21=1√2
P1P2=1√2
Similar Questions
Knowledge Check
A series LCR circuit has R=5Ω,L=40mH and C=1μF, the bandwidth of the circuit is
A10 HzB20 HzC30 HzD40 Hz
The power factor of the circuit in fig. is 1/√2. The capacitance of the circuit is equal to
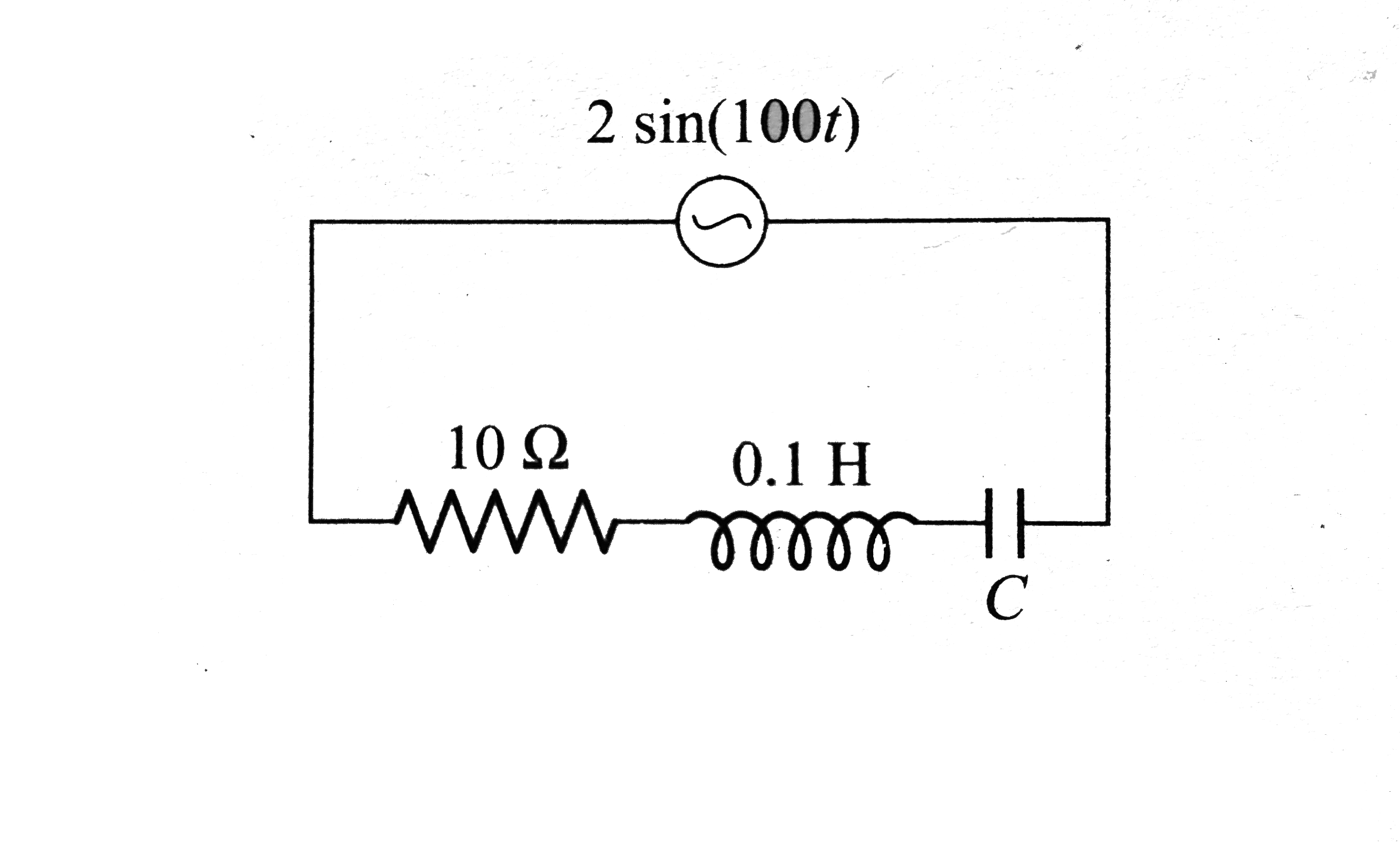
View SolutionIn a series R, L, C circuit XL=10Ω,Xc=4ωand R=6Ω. Find the power factor of the circuit
View SolutionFor a series L C R circuit, the power loss at resonance is
View SolutionFor a series L C R circuit, the power loss at resonance is
View SolutionIn a series LCR, AC circuit, if VL=800, VC=1600V and applied voltage is 1000V, then power factor is
View SolutionWhat is the value of power factor for series LR circuit ?
View SolutionIn an L-C-R series, AC circuit at resonance
View Solution
