two tangents RQ and RP are drawn from an external point R to the circle with centre O. If , then prove that OR= PR+ RQ
Step by step video & image solution for two tangents RQ and RP are drawn from an external point R to the circle with centre O. If /_PRQ =120^@ , then prove that OR= PR+ RQ by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two tangents PQ and PR are drawn from an external point to a circle with centre O. Prove that QORP is cyclic quadrilateral.
View SolutionTwo tangents PAandPB are drawn from an external point P to a circle with centre O. Prove that AOBP is a cyclic quadrilateral.
View SolutionIn the figure-3, from an external point P, two tangents PQ and PR are drawn to a circle of the radius 4 cm with centre O. If ∠ QPR = 90∘, then length of PQ is
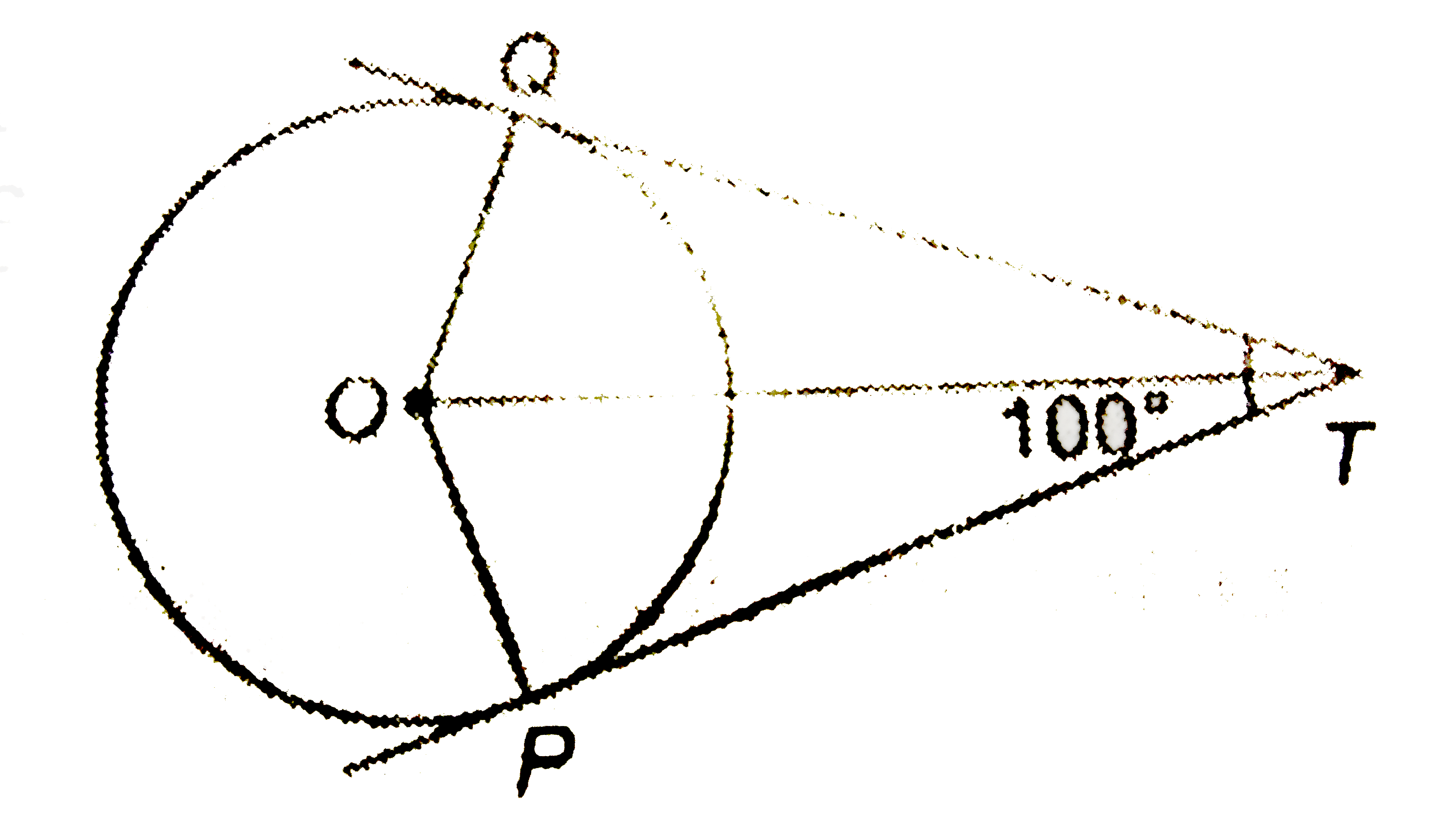
View SolutionTwo tangents TP and TQ are drawn from an external point T to a circle with centre O as shown in Fig. 10.73. If they are inclined to each other at an angle of 100o , then what is the value of ∠POQ ?
View SolutionTwo tangents TP and TQ are drawn from an external point T to a circle with centre O as shown in figure. If they are inclined to each other at an angle of 100∘, then what is the value of ∠POQ?
View SolutionIf Figure-1, from an external point P, two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O. if ∠QPR=90∘, then length of PQ is
View SolutionIn Figure, PA and PB are tangents from an external point P to a circle with centre O . LN touches the circle at M . Prove that PL+LM=PN+MN .
View SolutionIn Fig. 10.96, if TP and TQ are tangents drawn from an external points T to a circle with centre O such that ∠TQP=60o , then ∠OPQ= (FIGURE) 25o (b) 30o (c) 40o (d) 60o
View SolutionIn figure, From an external point P, Two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O . If ∠QPR=90∘ then length of PQ is
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View Solution