In Figure 3, AD⊥BC and BD=13CD. Prove that 2CA2=2AB2+BC2.
To prove that 2CA2=2AB2+BC2 given that AD⊥BC and BD=13CD, we can follow these steps:
Step 1: Express BC in terms of BD and CD
Since BC=BD+CD and we know that BD=13CD, we can express CD in terms of BC.
Let CD=x. Then, BD=13x.
Thus,
BC=BD+CD=13x+x=43x
From this, we can express CD as:
CD=34BC(Equation 1)
Step 2: Express BD in terms of BC
Using Equation 1:
BD=13CD=13(34BC)=14BC(Equation 2)
Step 3: Apply the Pythagorean theorem in triangles ADC and ADB
In triangle ADC:
AC2=AD2+CD2(Equation 3)
In triangle ADB:
AB2=AD2+BD2(Equation 4)
Step 4: Express AD2 from Equation 4
From Equation 4, we can express AD2:
AD2=AB2−BD2(Equation 5)
Step 5: Substitute AD2 into Equation 3
Substituting Equation 5 into Equation 3 gives:
AC2=(AB2−BD2)+CD2
Step 6: Substitute BD and CD from Equations 1 and 2
Substituting BD=14BC and CD=34BC:
AC2=AB2−(14BC)2+(34BC)2
Calculating the squares:
=AB2−116BC2+916BC2
=AB2+816BC2
=AB2+12BC2
Step 7: Multiply the entire equation by 2
Now, multiplying the entire equation by 2 gives:
2AC2=2AB2+BC2
Conclusion
Thus, we have proved that:
2CA2=2AB2+BC2
Since BC=BD+CD and we know that BD=13CD, we can express CD in terms of BC.
BC=BD+CD=13x+x=43x
From this, we can express CD as:
CD=34BC(Equation 1)
Using Equation 1:
BD=13CD=13(34BC)=14BC(Equation 2)
In triangle ADC:
AC2=AD2+CD2(Equation 3)
AB2=AD2+BD2(Equation 4)
From Equation 4, we can express AD2:
AD2=AB2−BD2(Equation 5)
Substituting Equation 5 into Equation 3 gives:
AC2=(AB2−BD2)+CD2
Substituting BD=14BC and CD=34BC:
AC2=AB2−(14BC)2+(34BC)2
Calculating the squares:
=AB2−116BC2+916BC2
=AB2+816BC2
=AB2+12BC2
Now, multiplying the entire equation by 2 gives:
2AC2=2AB2+BC2
Thus, we have proved that:
2CA2=2AB2+BC2
Topper's Solved these Questions
Similar Questions
In Figure 2,AD⊥BC. Prove that AB2+CD2=BD2+AC2.
View SolutionIn Figure DE||BC and CD||EF. Prove that AD2=AB⋅AF.
View SolutionThe perpendicular from A on side BC of a ABC intersects BC at D such that DB = 3 CD. Prove that 2AB2=2AC2+BC2.
View SolutionIn the following figure, OA=OC and AB=BC.
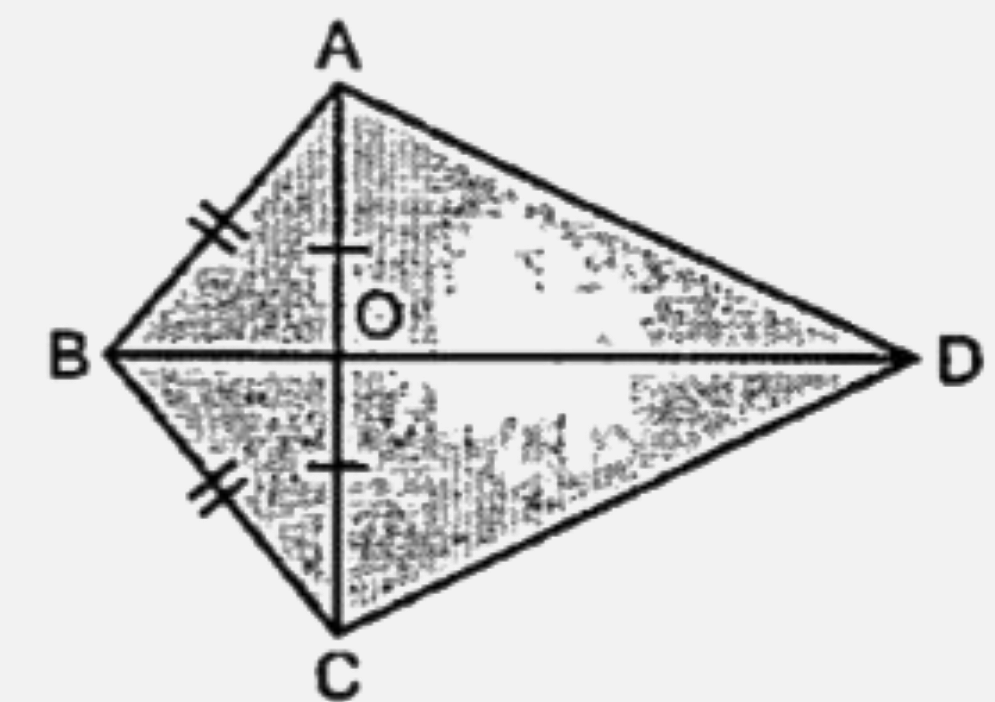
Prove that :
AD=CD
View SolutionP and Q are the mid-points of the CA and CD respectively of a triangle ABC, right angled at C. Prove that: 4AQ2=4AC2+ BC2, 4BP2=4BC2+AC2, and 4(AQ2+ BP2)=5AB2.
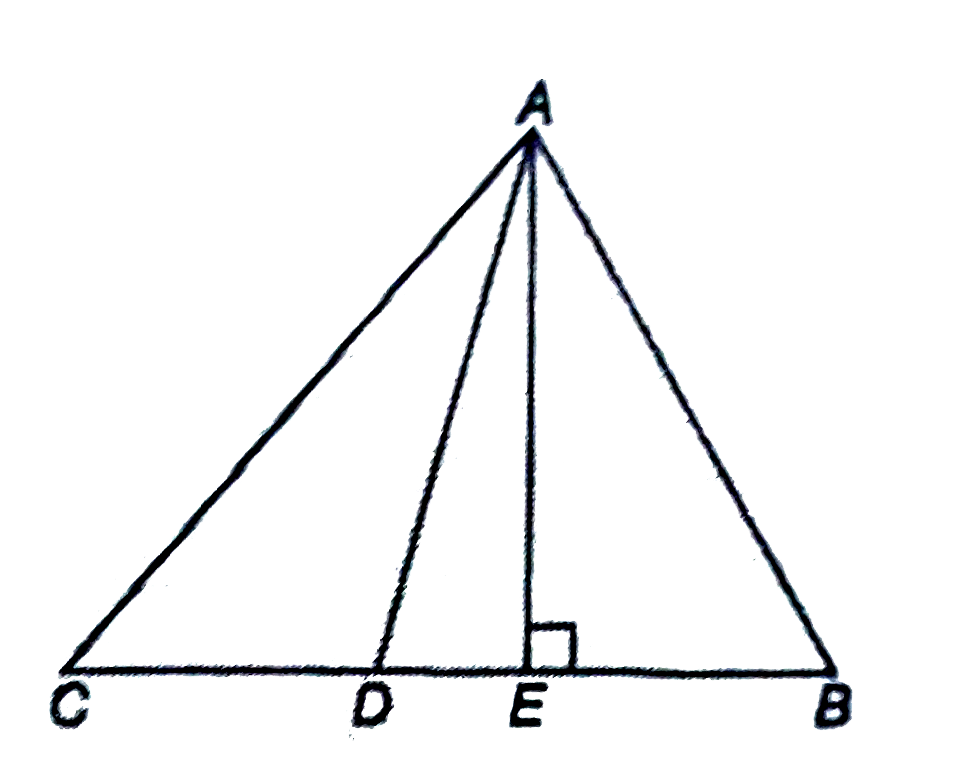
View SolutionThe following figure shows a triangle ABC in which AD is a median and AE⊥BC. Prove that 2AB2+2AC2=4AD2+BC2 .
View SolutionIn figure - 6 in an equilateral triangle ABC, AD⊥BC,BE⊥ACandCF⊥AB. Prove that 4(AD2+BE2+CF2)=9AB2

View SolutionIn an acute angled triangle ABC, AD is the median in it. then :
AD2 =
View SolutionIn the following figure , AB = BC , AD ⊥BCandCE⊥AB.prove that AD = CE
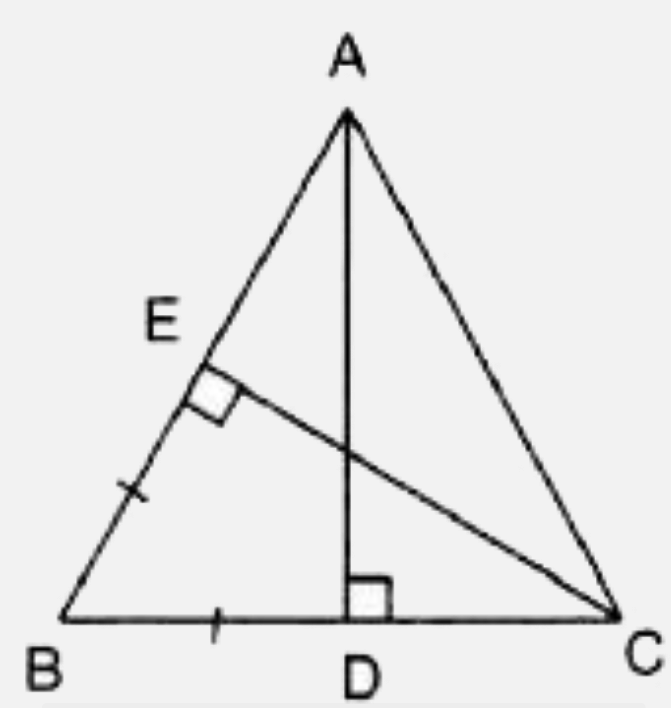
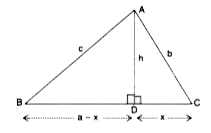
View SolutionIn the figure, given below, AD ⊥ BC.
Prove that : c2=a2+b2−2ax.
View Solution
