Draw a schematic diagram of circuit consisting of a battery of 3 cells of 2V each, combination of three resistors 10ohm, 20ohm and 30ohm connected in parallel, a plug key and an ammeter,all connected in series. Use this circuit to find the following
(i) Current through each resistor.
(ii) Total current in circuit
(iii)Total Effective resistance of circuit
Step-by-Step Solution
Step 1: Draw the Schematic Diagram
- Start by drawing the battery which consists of three cells of 2V each. This gives a total voltage of 6V (3 cells × 2V).
- Next, draw three resistors labeled as R1 (10 ohm), R2 (20 ohm), and R3 (30 ohm) connected in parallel.
- Connect an ammeter in series with the battery and the parallel combination of resistors.
- Include a plug key in the circuit to complete the circuit.
- The schematic diagram should look like this:
±−−(R1:10Ω)−−−+||±−−(R2:20Ω)−−−±−−(Ammeter)−−−(PlugKey)−−−(Baery:6V)||±−−(R3:30Ω)−−−+
Step 2: Calculate Current through Each Resistor
- Since the resistors are in parallel, the voltage across each resistor is the same and equal to the total voltage of the battery, which is 6V.
1. Current through R1 (I1):
\(
I_1 = \frac{V}{R_1} = \frac{6V}{10Ω} = 0.6A
\)
2. Current through R2 (I2):
\(
I_2 = \frac{V}{R_2} = \frac{6V}{20Ω} = 0.3A
\)
3. Current through R3 (I3):
\(
I_3 = \frac{V}{R_3} = \frac{6V}{30Ω} = 0.2A
\)
Step 3: Calculate Total Current in the Circuit
- The total current (I) from the battery is the sum of the currents through each resistor:
\(
I = I_1 + I_2 + I_3 = 0.6A + 0.3A + 0.2A = 1.1A
\)
Step 4: Calculate Total Effective Resistance of the Circuit
- The total effective resistance (R_eq) for resistors in parallel can be calculated using the formula:
\(
\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}
\)
\(
\frac{1}{R_{eq}} = \frac{1}{10} + \frac{1}{20} + \frac{1}{30}
\)
- Finding a common denominator (60):
\(
\frac{1}{R_{eq}} = \frac{6}{60} + \frac{3}{60} + \frac{2}{60} = \frac{11}{60}
\)
- Therefore, the effective resistance is:
\(
R_{eq} = \frac{60}{11} \approx 5.45Ω
\)
Summary of Results
- Current through R1: 0.6 A
- Current through R2: 0.3 A
- Current through R3: 0.2 A
- Total current in the circuit: 1.1 A
- Total effective resistance of the circuit: \( \frac{60}{11} \) ohms or approximately 5.45 ohms
- Start by drawing the battery which consists of three cells of 2V each. This gives a total voltage of 6V (3 cells × 2V).
- Next, draw three resistors labeled as R1 (10 ohm), R2 (20 ohm), and R3 (30 ohm) connected in parallel.
- Connect an ammeter in series with the battery and the parallel combination of resistors.
- Include a plug key in the circuit to complete the circuit.
- The schematic diagram should look like this:
- Since the resistors are in parallel, the voltage across each resistor is the same and equal to the total voltage of the battery, which is 6V.
1. Current through R1 (I1):
\(
I_1 = \frac{V}{R_1} = \frac{6V}{10Ω} = 0.6A
\)
\(
I_2 = \frac{V}{R_2} = \frac{6V}{20Ω} = 0.3A
\)
\(
I_3 = \frac{V}{R_3} = \frac{6V}{30Ω} = 0.2A
\)
- The total current (I) from the battery is the sum of the currents through each resistor:
\(
I = I_1 + I_2 + I_3 = 0.6A + 0.3A + 0.2A = 1.1A
\)
- The total effective resistance (R_eq) for resistors in parallel can be calculated using the formula:
\(
\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}
\)
\(
\frac{1}{R_{eq}} = \frac{1}{10} + \frac{1}{20} + \frac{1}{30}
\)
- Finding a common denominator (60):
\(
\frac{1}{R_{eq}} = \frac{6}{60} + \frac{3}{60} + \frac{2}{60} = \frac{11}{60}
\)
- Therefore, the effective resistance is:
\(
R_{eq} = \frac{60}{11} \approx 5.45Ω
\)
- Current through R1: 0.6 A
- Current through R2: 0.3 A
- Current through R3: 0.2 A
- Total current in the circuit: 1.1 A
- Total effective resistance of the circuit: \( \frac{60}{11} \) ohms or approximately 5.45 ohms
Similar Questions
Draw a schematic diagram of a circuit consisting of a battery of three cells of 2V each, a 5 ohm resistor, an 8 ohm resistor, and a 12 ohm resistor, and a plug key, all connected in series.
View SolutionVoltmeter V and Ammeter A are used to measure the total potential difference of the circuit and the current through each resistor. Which is the correct circuit ?

View Solution
Knowledge Check
Three resistors of resistances 3Ω,4Ωand5Ω are combined in parallel. This combination is connected to a battery of emf 12V and negligible internal resistance, current through each resistor in ampere is
A4,3,2.4B8,7,3,4C2,5,1,8D5,5,8,2
In the circuit diagram given below, three resistors R1,R2, and R3 of 5Ω,10Ω and 30Ω, respectively are connected as shown.

Calculate:
(a) current through each resistor.
(b) total current in the circuit.
(c) total resistance in the circuit.
View SolutionThe electric current through 10 ohm resistor in circuit given below is
View SolutionTwo resistors of 2.0 92 and 3.0 22 are connected
in parallel, with a battery of 60 V and negligible internal resistance. For each case draw a circuit diagram and calculate the current through the battery
View SolutionTwo resistors of 4 Ω and 6 Ω are connected in parallel. The combination is connected across a 6 V battery of negligible resistance. (i) Draw a circuit diagram. (ii) Calculate :the current through each resistor
View SolutionThree initially uncharged capacitors are connected in series as shown in circuit with a battery of emf 30V. Find out following :
(i) charge flow through the battery,
(ii) potential energy in 3μF capacitor.
(iii) Utotal in capacitors
(iv) heat produced in the circuit
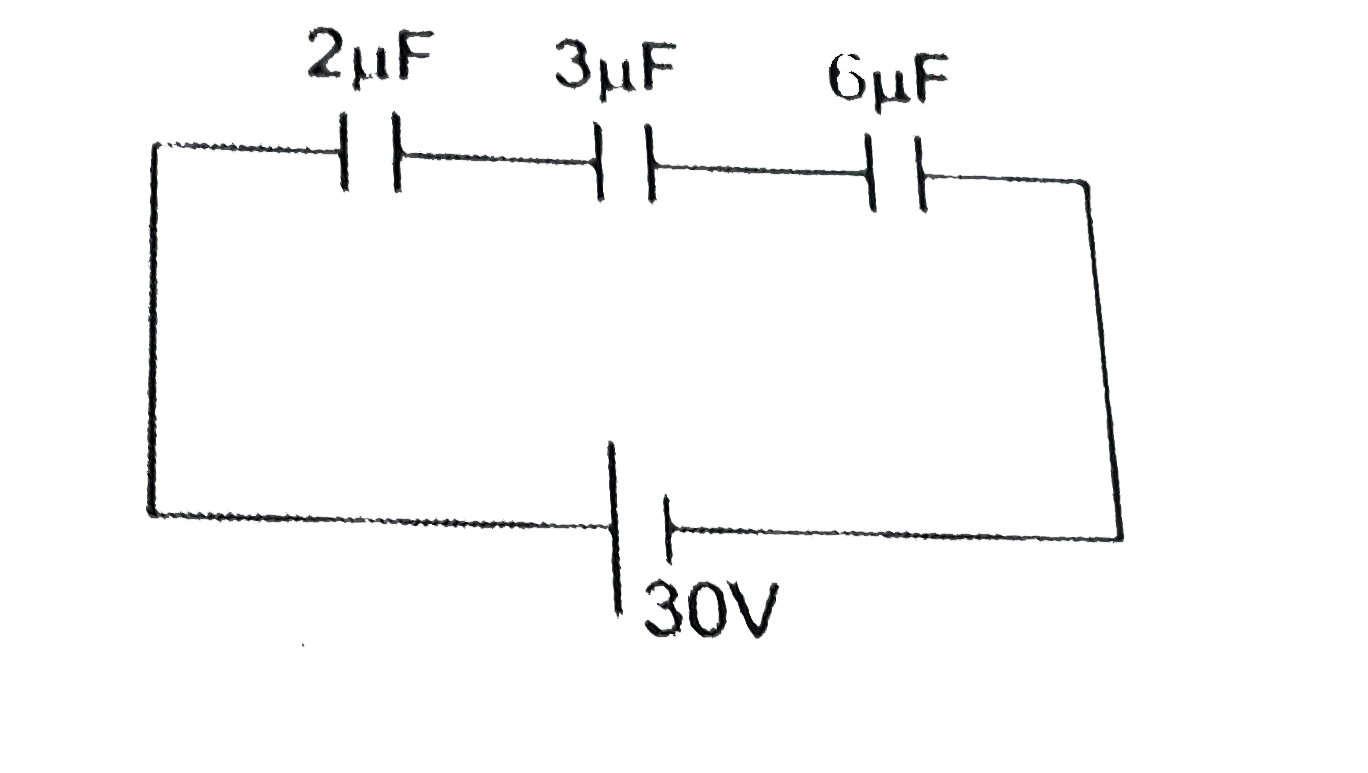
View SolutionResistors of 1, 2, 3 ohm are connected in the form of a triangle. If a 1.5V cell of negligible internal resistance is connected across 3 ohm resistor, the current flowing through this resistance will be
View SolutionA combination consists of three resistors in series. Four similar sets are connected in parallel. If the resistance of each resistor is 2 Ω, find the resistance of the combination.
View Solution
