Question

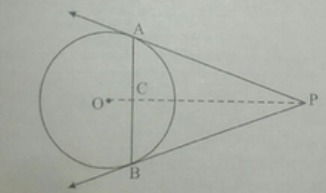
In the figure-3, from an external point P, two tangents PQ and PR are drawn to a circle of the radius 4 cm with centre O. If $\angle$ QPR = ${90}^{\circ }$, then length of PQ is

Explanation

To solve the problem, we need to find the length of the tangent PQ drawn from an external point P to a circle with a radius of 4 cm, given that the angle QPR is 90 degrees.

1. Understand the Geometry:
- We have a circle with center O and radius 4 cm.
- From point P (external to the circle), two tangents PQ and PR are drawn to the circle.
- The angle QPR is given as 90 degrees.

2. Identify the Key Properties of Tangents:
- The tangent to a circle is perpendicular to the radius at the point of tangency. Therefore, OQ (radius to point Q) is perpendicular to PQ, and OR (radius to point R) is perpendicular to PR.

3. Label the Angles:
- Since OQ is perpendicular to PQ, we have angle OQP = 90 degrees.
- Similarly, since OR is perpendicular to PR, we have angle ORP = 90 degrees.

4. Analyze the Quadrilateral OQPR:
- We know that OQ = OR (both are radii of the circle, which are equal).
- We have angle QPR = 90 degrees, and both angles OQP and ORP are also 90 degrees.
- Thus, quadrilateral OQPR forms a right angle at P.

5. Conclude the Shape:
- Since all angles are right angles and two sides (OQ and OR) are equal, quadrilateral OQPR is a square.
- In a square, all sides are equal.

6. Calculate the Length of PQ:
- The length of the radius OQ is given as 4 cm.
- Therefore, since OQ = PQ (as all sides of the square are equal), we conclude that:
\( PQ = OQ = 4 \text{ cm} \)

Final Answer:
The length of PQ is 4 cm.