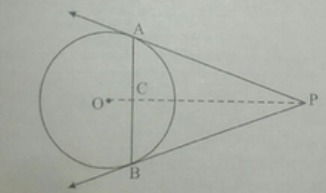
In Figure, there are two concentric circles with centre of radii . From an external point tangents are drawn to these circles. If find the length of
To solve the problem, we need to find the length of BP given the lengths of the tangents from an external point P to two concentric circles with radii 5cm and 3cm.
1. Identify the Given Information:
- Radius of the larger circle OA=5cm
- Radius of the smaller circle OB=3cm
- Length of tangent AP=12cm
2. Construct the Diagram:
- Draw two concentric circles with center O.
- Mark point P outside the circles.
- Draw tangents PA to the larger circle and PB to the smaller circle.
3. Apply the Pythagorean Theorem in Triangle OAP:
- Since OA is the radius and PA is a tangent, triangle OAP is a right triangle.
- By the Pythagorean theorem:
OP2=OA2+AP2
- Substitute the known values:
OP2=52+122
OP2=25+144
OP2=169
- Taking the square root gives:
OP=√169=13cm
4. Apply the Pythagorean Theorem in Triangle OBP:
- Similarly, triangle OBP is also a right triangle.
- By the Pythagorean theorem:
OP2=OB2+BP2
- Substitute the known values:
132=32+BP2
169=9+BP2
- Rearranging gives:
BP2=169−9
BP2=160
- Taking the square root gives:
BP=√160=√16×10=4√10cm
5. Final Answer:
- The length of BP is 4√10cm.
- Radius of the larger circle OA=5cm
- Radius of the smaller circle OB=3cm
- Length of tangent AP=12cm
- Draw two concentric circles with center O.
- Mark point P outside the circles.
- Draw tangents PA to the larger circle and PB to the smaller circle.
- Since OA is the radius and PA is a tangent, triangle OAP is a right triangle.
- By the Pythagorean theorem:
OP2=OA2+AP2
- Substitute the known values:
OP2=52+122
OP2=25+144
OP2=169
- Taking the square root gives:
OP=√169=13cm
- Similarly, triangle OBP is also a right triangle.
- By the Pythagorean theorem:
OP2=OB2+BP2
- Substitute the known values:
132=32+BP2
169=9+BP2
- Rearranging gives:
BP2=169−9
BP2=160
- Taking the square root gives:
BP=√160=√16×10=4√10cm
- The length of BP is 4√10cm.
Topper's Solved these Questions
Similar Questions
In the given figure two concentric circles with centre O are of radii 5 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circles. If AP =12 cm find BP.

View SolutionFrom an external point P, two tangents PA and PB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of AB.
View SolutionFrom a point P, two tangents PA and PB are drawn such that PA=10 cm and ∠APB=60∘. Find the length of chord AB.
View SolutionTwo circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of common chord PQ.
View SolutionIn the figure-3, from an external point P, two tangents PQ and PR are drawn to a circle of the radius 4 cm with centre O. If ∠ QPR = 90∘, then length of PQ is
View SolutionIn Figure, there are two concentric circles with centre O . PR and PQS are tangents to the inner circle from point plying on the outer circle. If PR=7.5cm , then PS is equal to (a) 10cm (b) 12cm (c) 15cm (d) 18cm
View SolutionIn figure, From an external point P, Two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O . If ∠QPR=90∘ then length of PQ is
View SolutionTwo concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionTwo concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
View SolutionTwo concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
View Solution