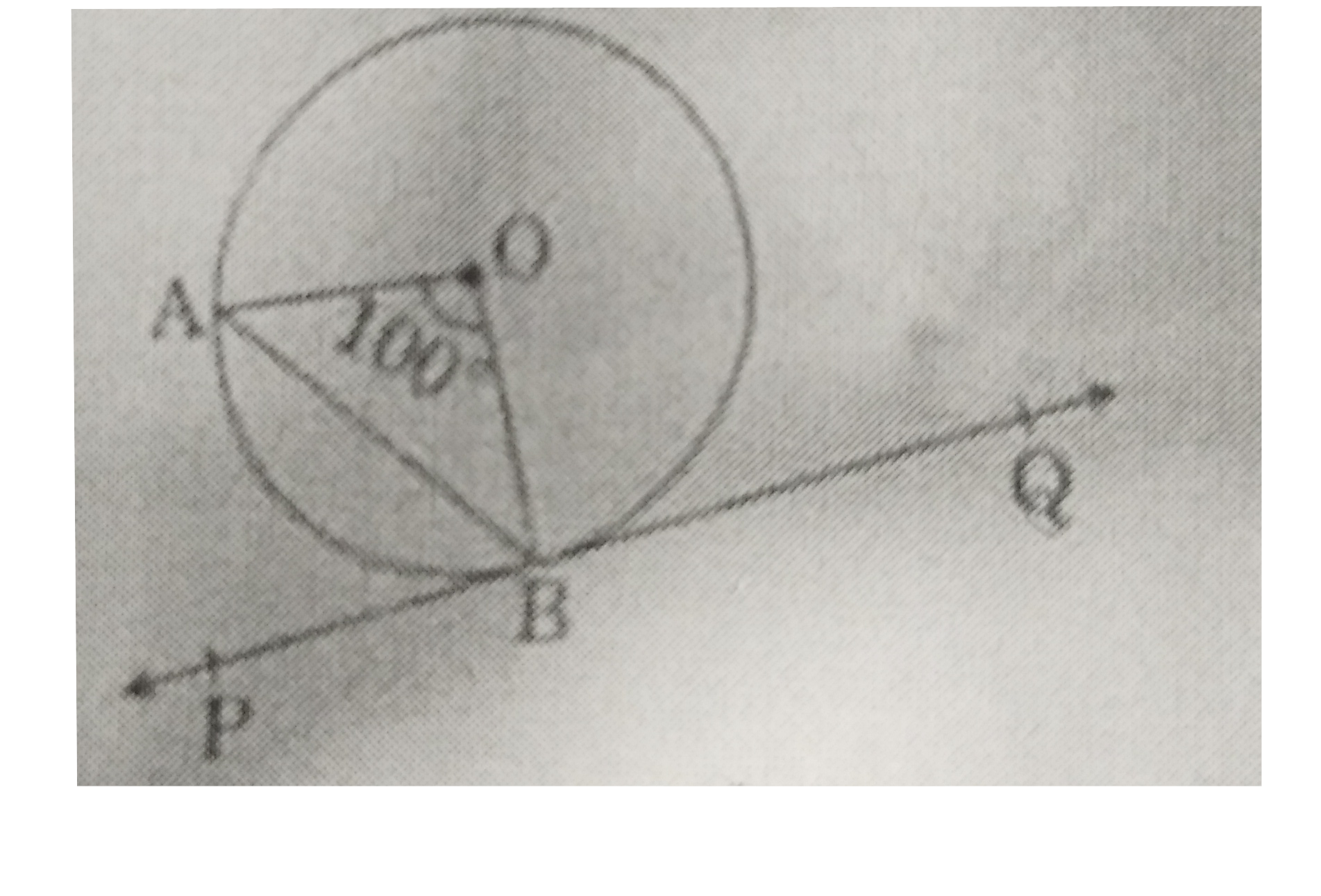
In Figure-2 PQ is tangent to the circle with centre at O , at the point B. If ∠AOB = 100∘ , then ∠ABP is equal to
(A) 50∘
(B) 40∘
(C) 60∘
(D) 80∘
To solve the problem, we need to find the measure of angle ABP given that angle AOB is 100 degrees and PQ is tangent to the circle at point B.
1. Identify the Given Information:
- Angle AOB = 100 degrees
- PQ is tangent to the circle at point B.
2. Recognize Triangle OAB:
- Since O is the center of the circle and A and B are points on the circle, OA and OB are radii of the circle. Therefore, OA = OB.
3. Determine Triangle Type:
- Triangle OAB is an isosceles triangle because two sides (OA and OB) are equal.
4. Set Angles in Triangle OAB:
- Let angle OAB = angle OBA = x (since the angles opposite equal sides in an isosceles triangle are equal).
- The sum of angles in triangle OAB is 180 degrees:
x+x+100=180
- This simplifies to:
2x+100=180
- Subtract 100 from both sides:
2x=80
- Divide by 2:
x=40 degrees
5. Determine Angle OBP:
- Since PQ is tangent to the circle at point B, angle OBP is 90 degrees (the radius is perpendicular to the tangent at the point of tangency).
6. Use the Angle Sum Property:
- In triangle OBP, we have:
Angle OBP=Angle OBA+Angle ABP
- We know angle OBP = 90 degrees and angle OBA = 40 degrees.
- Therefore:
90=40+Angle ABP
- Rearranging gives:
Angle ABP=90−40=50 degrees
Final Answer:
- The measure of angle ABP is 50 degrees.
- Angle AOB = 100 degrees
- PQ is tangent to the circle at point B.
- Since O is the center of the circle and A and B are points on the circle, OA and OB are radii of the circle. Therefore, OA = OB.
- Triangle OAB is an isosceles triangle because two sides (OA and OB) are equal.
- Let angle OAB = angle OBA = x (since the angles opposite equal sides in an isosceles triangle are equal).
- The sum of angles in triangle OAB is 180 degrees:
x+x+100=180
- This simplifies to:
2x+100=180
- Subtract 100 from both sides:
2x=80
- Divide by 2:
x=40 degrees
- Since PQ is tangent to the circle at point B, angle OBP is 90 degrees (the radius is perpendicular to the tangent at the point of tangency).
- In triangle OBP, we have:
Angle OBP=Angle OBA+Angle ABP
- We know angle OBP = 90 degrees and angle OBA = 40 degrees.
- Therefore:
90=40+Angle ABP
- Rearranging gives:
Angle ABP=90−40=50 degrees
- The measure of angle ABP is 50 degrees.
Similar Questions
In figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to
View SolutionIn figure PQ is tangent to the circle with centre at O at the point B , if ∠AOB=100∘, then ∠ABP is equal to

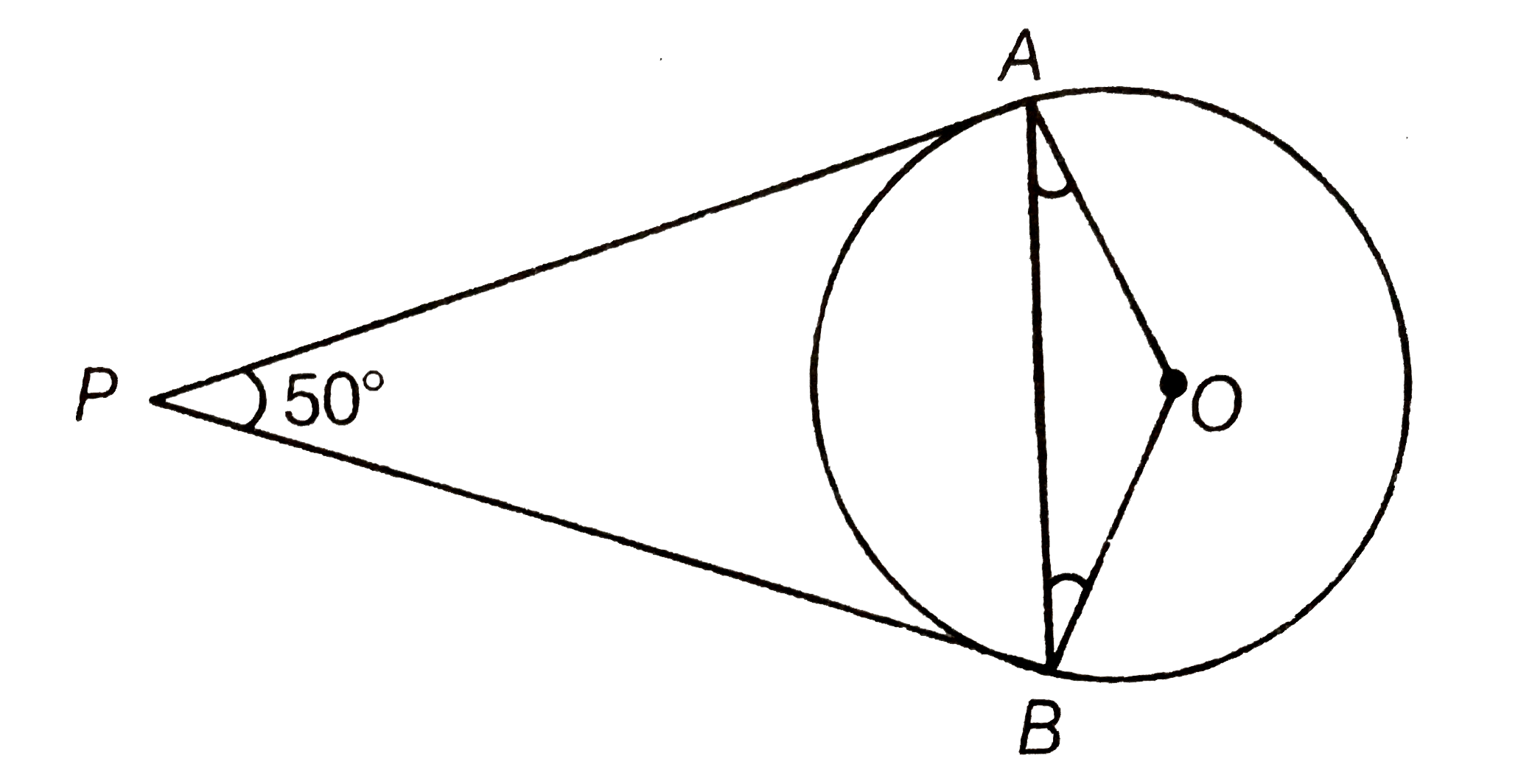
View SolutionIn figure, if PA and PB are tangents to the circle with centre O such that ∠APB=50∘, then ∠OAB is equal to
View SolutionIn the given figure, if TP and TQ are tangents to a circle with centre O, so that ∠POQ=110∘, then ∠PTQ is
View SolutionIn Figure 2, AB and AC are tangents to the circle with centre O such that angle BAC = 40°. Then angle BOC is equal to
View SolutionIn Figure, APB is a tangent to a circle with centre O at point P . If ∠QPB=50∘ , then the measure of ∠POQ is (a)100∘ (b) 120∘ (c) 140∘ (d) 150∘
View SolutionIn Figure, O is the centre of the circle. Find ∠CBD
View SolutionIn Figure, O is the centre of the circle. Find ∠BAC
View SolutionIn Figure, BC is a tangent to the circle with centre O.OE bisects AP. Prove that AEO~ABC.
View SolutionIn Figure, PA and PB are tangents to the circle with centre O such that ∠APB=50∘ . Write the measure of ∠OAB .
View Solution
