In Figure, BC is a tangent to the circle with centre O.OE bisects AP. Prove that AEO~ABC.
To prove that triangle AEO is similar to triangle ABC, we will follow these steps:
Step 1: Identify the given information
We know that BC is a tangent to the circle at point E, and OE bisects AP.
Step 2: Establish the properties of the tangent
Since BC is a tangent to the circle at point E, we know that the radius OE is perpendicular to the tangent line BC. Therefore, we have:
∠OEB=90∘
Step 3: Analyze the triangle AEO
In triangle AEO:
- OE is a radius of the circle.
- OA is also a radius of the circle.
Thus, we have:
OA=OE
Step 4: Analyze the triangle ABC
In triangle ABC:
- Since BC is tangent to the circle at E, we also have:
∠ABC=90∘
Step 5: Establish the common angle
Both triangles AEO and ABC share the angle A (i.e., ∠AEO and ∠ABC).
Step 6: Use the Angle-Angle (AA) similarity criterion
Now we have:
1. ∠OEB=90∘ (from the tangent property)
2. ∠ABC=90∘ (from the tangent property)
3. ∠AEO is common to both triangles.
Since two angles in triangle AEO are equal to two angles in triangle ABC, by the Angle-Angle (AA) similarity criterion, we can conclude:
△AEO∼△ABC
Conclusion
Thus, we have proved that triangle AEO is similar to triangle ABC.
---
We know that BC is a tangent to the circle at point E, and OE bisects AP.
Since BC is a tangent to the circle at point E, we know that the radius OE is perpendicular to the tangent line BC. Therefore, we have:
∠OEB=90∘
In triangle AEO:
- OE is a radius of the circle.
- OA is also a radius of the circle.
Thus, we have:
OA=OE
In triangle ABC:
- Since BC is tangent to the circle at E, we also have:
∠ABC=90∘
Both triangles AEO and ABC share the angle A (i.e., ∠AEO and ∠ABC).
Now we have:
1. ∠OEB=90∘ (from the tangent property)
2. ∠ABC=90∘ (from the tangent property)
3. ∠AEO is common to both triangles.
△AEO∼△ABC
Thus, we have proved that triangle AEO is similar to triangle ABC.
Topper's Solved these Questions
Similar Questions
In Figure, O is the centre of the circle. Find ∠BAC
View SolutionIn Figure, O is the centre of the circle. Find ∠CBD
View SolutionTwo circles with centres O and O'are drawn to intersect each other at points A and B. Centre O of one circle lies on the circumference of the other circle and CD is drawn tangent to the circle with centre O' at A. prove that OA bisects angle BAC.

View SolutionIn Figure, O is the centre of the circle and BCD is tangent to it at C. Prove that ∠BAC+∠ACD=900 .
View SolutionIn Figure, two tangents ABandAC are drawn to a circle with centre O such that ∠BAC=1200. Prove that OA=2AB
View SolutionIn Figure, PA and PB are tangents to the circle with centre O such that ∠APB=50∘ . Write the measure of ∠OAB .
View SolutionIn a figure the common tangents, AB and CD to two circles with centers O and O' intersect at E. Prove that the points O, E and O' are collinear.
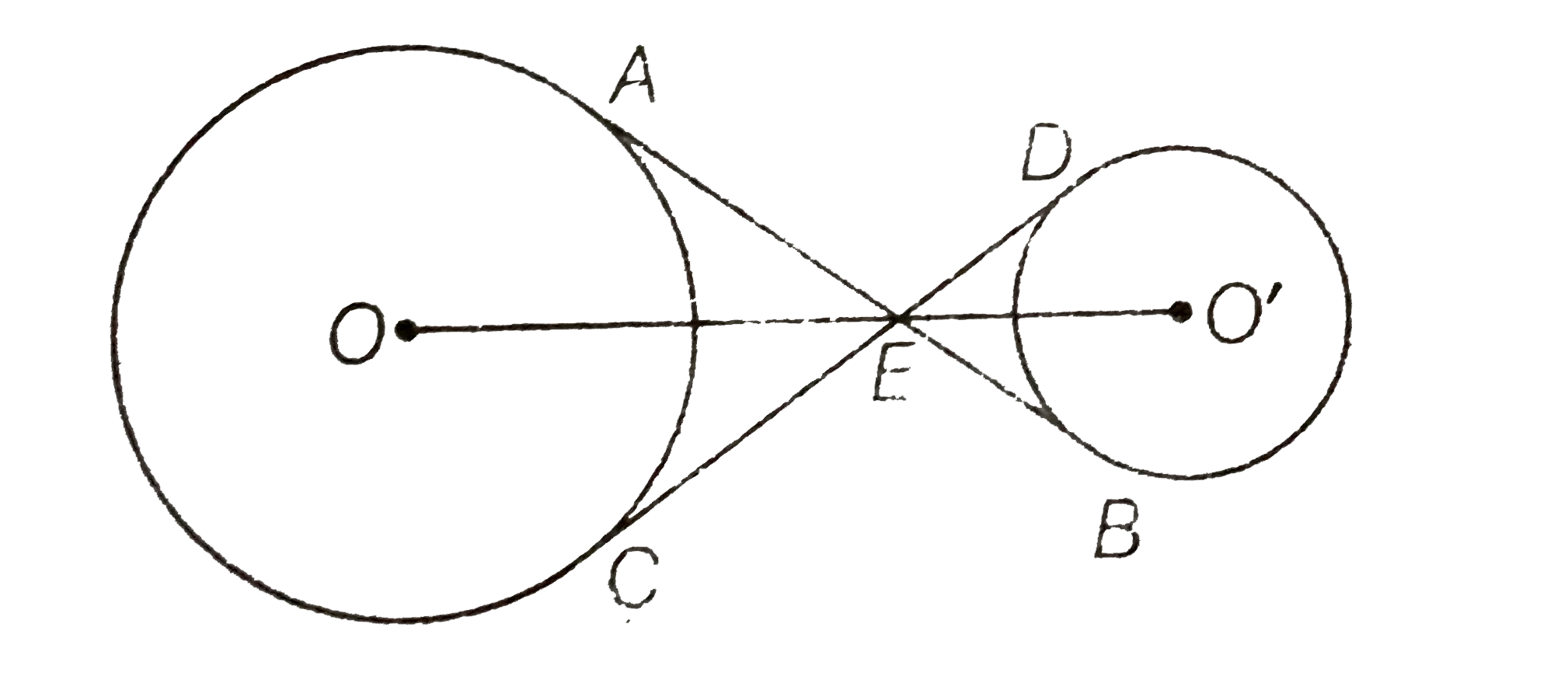
View SolutionIn Figure, AB=CB and O is the centre of the circle. Prove that BO bisects ∠ABC.
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionTwo tangent segments PA and PB are drawn to a circle with centre O such that ∠APB=120∘ . Prove that OP=2 AP .
View Solution