Let P(x)=x2+bx+cwherebandc are integer. If P(x) is a factor of both x4+6x2+25and3x4+4x2+28x+5,then a.P(x)=0 has imaginary roots b.P(x)=0 has roots of opposite c.P(1)=4 d .P(1)=6
To solve the problem, we need to determine the polynomial P(x)=x2+bx+c that is a factor of both x4+6x2+25 and 3x4+4x2+28x+5. We will follow these steps:
Step 1: Identify the polynomials
We have:
1. f(x)=x4+6x2+25
2. g(x)=3x4+4x2+28x+5
Step 2: Find the GCD of the two polynomials
Since P(x) is a common factor, we can find the GCD of f(x) and g(x). We will use polynomial long division.
Step 3: Divide g(x) by f(x)
Perform polynomial long division of g(x) by f(x):
1. Divide the leading term of g(x) by the leading term of f(x):
3x4x4=3
2. Multiply f(x) by 3:
3(x4+6x2+25)=3x4+18x2+75
3. Subtract this from g(x):
g(x)−(3x4+18x2+75)=(3x4+4x2+28x+5)−(3x4+18x2+75)
This simplifies to:
−14x2+28x−70
Step 4: Factor the remainder
Now we need to factor −14x2+28x−70:
−14(x2−2x+5)
Step 5: Identify P(x)
From the factorization, we have:
P(x)=x2−2x+5
Here, b=−2 and c=5.
Step 6: Check the conditions
Now we will check the conditions given in the problem:
1. Imaginary roots: The discriminant of P(x) is:
D=b2−4ac=(−2)2−4(1)(5)=4−20=−16
Since D<0, P(x)=0 has imaginary roots.
2. Roots of opposite signs: Since the roots are imaginary, they cannot be of opposite signs.
3. Evaluate P(1):
P(1)=12−2(1)+5=1−2+5=4
4. Evaluate P(1) for the other condition:
We already found P(1)=4, so P(1)=6 is not satisfied.
Conclusion
The correct answer is:
- P(x)=0 has imaginary roots (Option a).
- P(1)=4 (Option c).
We have:
1. f(x)=x4+6x2+25
2. g(x)=3x4+4x2+28x+5
Since P(x) is a common factor, we can find the GCD of f(x) and g(x). We will use polynomial long division.
Perform polynomial long division of g(x) by f(x):
3x4x4=3
2. Multiply f(x) by 3:
3(x4+6x2+25)=3x4+18x2+75
3. Subtract this from g(x):
g(x)−(3x4+18x2+75)=(3x4+4x2+28x+5)−(3x4+18x2+75)
This simplifies to:
−14x2+28x−70
Now we need to factor −14x2+28x−70:
−14(x2−2x+5)
From the factorization, we have:
P(x)=x2−2x+5
Here, b=−2 and c=5.
Now we will check the conditions given in the problem:
D=b2−4ac=(−2)2−4(1)(5)=4−20=−16
Since D<0, P(x)=0 has imaginary roots.
P(1)=12−2(1)+5=1−2+5=4
We already found P(1)=4, so P(1)=6 is not satisfied.
The correct answer is:
- P(x)=0 has imaginary roots (Option a).
- P(1)=4 (Option c).
Topper's Solved these Questions
Similar Questions
Knowledge Check
If p(x)=4x−6andp(a)=0, then a=
A−6B−32C32D23
If f(x)=(p−xn)1n ,p>0 andn is a positive integer then f[f(x)] is equal to
View SolutionA quadratic trinomial P(x)=ax2+bx+c is such that the equation P(x)=x has no real roots. Prove that in this case equation P(P(x))=x has no real roots either.
View SolutionA quadratic trinomial P(x)=ax2+bx+c is such that the equation P(x)=x has o real roots. Prove that in this case equation P(P(x))=x has no real roots either.
View SolutionIf x,1,andz are in A.P. and x,2,andz are in G.P., then prove that x,and4,z are in H.P.
View SolutionIf x,1,andz are in A.P. and x,2,andz are in G.P., then prove that x,and4,z are in H.P.
View SolutionIn the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
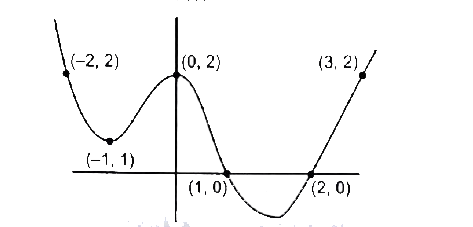
The product of all imaginary roots of p(x)=0 is:
View SolutionLeg P(x)=|76x−102x−105x−1034|, sum of zeroes of P(x) is
(a) 30
(b) 28
(c) 27
(d) None of these
View Solution
