Question

Let $f\left(x\right)=a{x}^2+bx+\cdot$
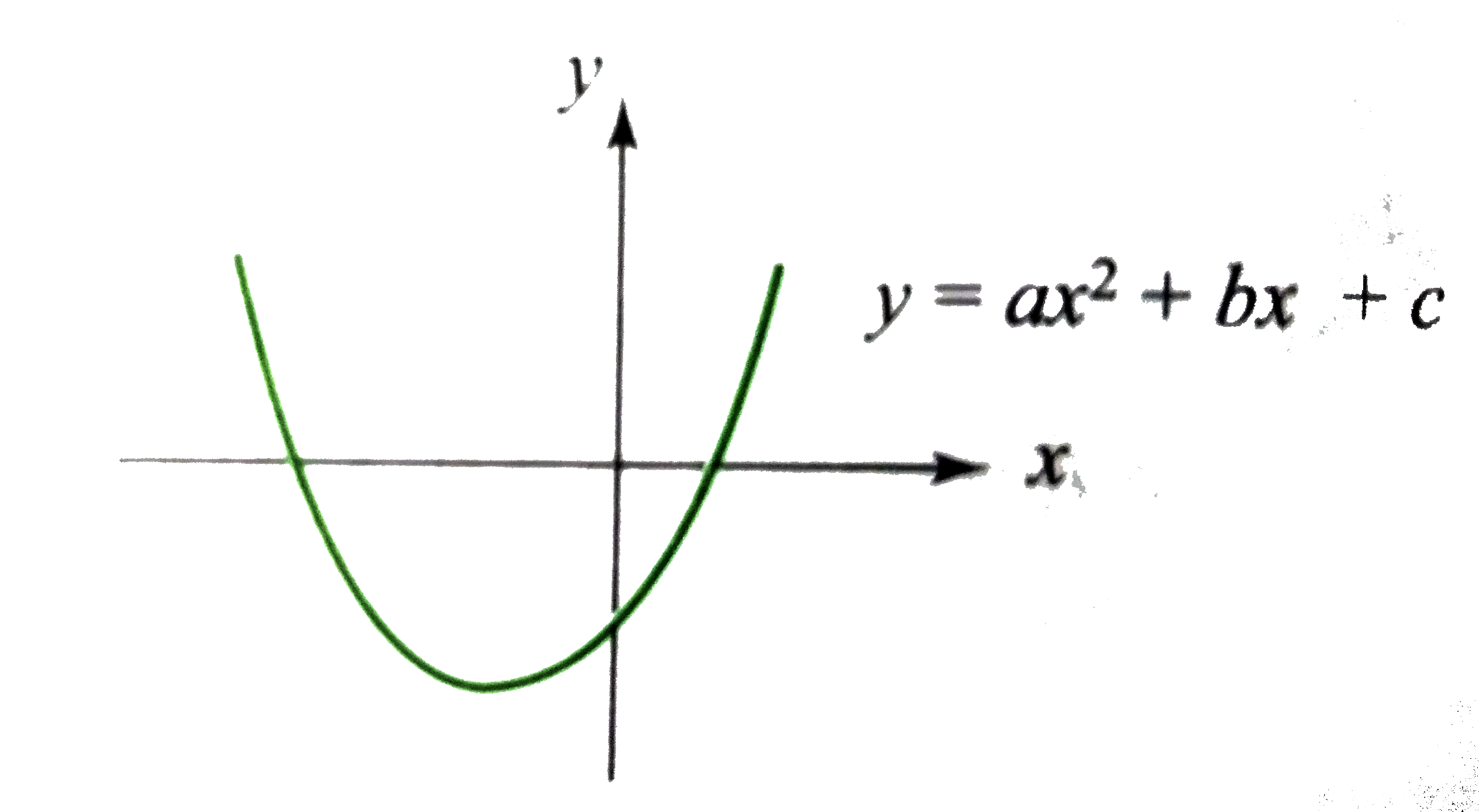
Consider the following diagram. Then
Fig
$c<0$

$b>0$

$a+b-c>0$

$abc<0$

Explanation

To solve the problem, we need to find the midpoint of the chord QR formed by the intersection of the tangent to the parabola $$y^2=8x$$ at the point (2, 4) and the parabola $$y^2=8x+5$$. Here are the steps to arrive at the solution:

Step 1: Write down the equations of the parabolas
The equations of the parabolas are:
1. \(y^2 = 8x\) (Equation 1)
2. \(y^2 = 8x + 5\) (Equation 2)

Step 2: Find the equation of the tangent at the point (2, 4)
The general form of the tangent to the parabola \(y^2 = 4ax\) at the point \((x_1, y_1)\) is given by:
\( yy_1 = 2a(x + x_1) \)
For the parabola \(y^2 = 8x\), we have \(a = 2\) (since \(4a = 8\)). Substituting \(x_1 = 2\) and \(y_1 = 4\):
\( y \cdot 4 = 8(x + 2) \)
Simplifying this, we get:
\( 4y = 8x + 16 \quad \Rightarrow \quad y = 2x + 4 \quad \text{(Equation 3)} \)

Step 3: Find the points of intersection of Equation 3 and Equation 2
Substituting \(y = 2x + 4\) into Equation 2:
\( (2x + 4)^2 = 8x + 5 \)
Expanding the left side:
\( 4x^2 + 16x + 16 = 8x + 5 \)
Rearranging gives:
\( 4x^2 + 8x + 11 = 0 \)

Step 4: Solve the quadratic equation for x
Using the quadratic formula \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\):
Here, \(a = 4\), \(b = 8\), and \(c = 11\):
\( x = \frac{-8 \pm \sqrt{8^2 - 4 \cdot 4 \cdot 11}}{2 \cdot 4} \)
Calculating the discriminant:
\( b^2 - 4ac = 64 - 176 = -112 \)
Since the discriminant is negative, there are no real solutions for \(x\). This indicates that the tangent does not intersect the second parabola.

Step 5: Conclusion
Since the tangent does not intersect the second parabola, we cannot find points Q and R, and thus cannot find the midpoint of the chord QR.