How many geometric progressions are possible containing 27, 8 and 12 as three of its/their terms
To determine how many geometric progressions (GPs) can be formed with the terms 27, 8, and 12, we can follow these steps:
Step 1: Identify the ratios
First, we need to find the ratios between the terms.
Let:
- a=8
- b=12
- c=27
We calculate the ratios:
- R1=ba=128=32
- R2=cb=2712=94
Step 2: Check the relationship between the ratios
Next, we check if the ratios maintain a consistent relationship that would allow for a GP. We can express R2 in terms of R1:
We see that:
- R21=(32)2=94=R2
This shows that the ratio between the terms is consistent with the properties of a geometric progression.
Step 3: Determine the number of terms
In a geometric progression, if we have three terms, we can insert additional terms between them. The number of terms that can be added between any two terms in a GP is infinite.
Specifically, if we denote:
- n as the number of terms we can add between 8 and 12,
- m as the number of terms we can add between 12 and 27,
Then the total number of terms in the GP can be expressed as:
- Total terms = n+3+m (where 3 accounts for the original terms 8, 12, and 27).
Conclusion
Since we can add any number of terms n and m (including zero), there are infinitely many geometric progressions that can be formed containing 27, 8, and 12 as terms.
Final Answer
Thus, the number of geometric progressions possible containing 27, 8, and 12 as three of its terms is infinite.
---
First, we need to find the ratios between the terms.
- a=8
- b=12
- c=27
- R1=ba=128=32
- R2=cb=2712=94
Next, we check if the ratios maintain a consistent relationship that would allow for a GP. We can express R2 in terms of R1:
- R21=(32)2=94=R2
In a geometric progression, if we have three terms, we can insert additional terms between them. The number of terms that can be added between any two terms in a GP is infinite.
- n as the number of terms we can add between 8 and 12,
- m as the number of terms we can add between 12 and 27,
- Total terms = n+3+m (where 3 accounts for the original terms 8, 12, and 27).
Since we can add any number of terms n and m (including zero), there are infinitely many geometric progressions that can be formed containing 27, 8, and 12 as terms.
Thus, the number of geometric progressions possible containing 27, 8, and 12 as three of its terms is infinite.
Topper's Solved these Questions
Similar Questions
How many geometrical isomers are possible for

View SolutionDoes there exist a geometric progression containing 27,8 and 12 as three of its term ? If it exists, then how many such progressions are possible ?
View Solution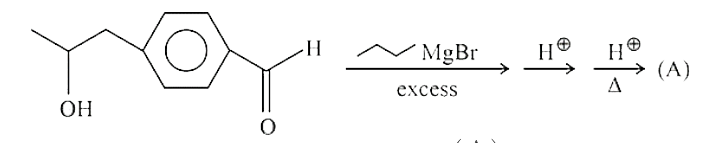
How many geometrical isomer of (A) is possible?
View SolutionAssertion: There are infinite geometric progressions of for which 27,8 and 12 are three of its terms (not necessarily consecutive). Reason: Given terms are integers. (A) Both assertion and reason are correct and Reason is the correct explanation of assertion. (B) Both assertion and reason are correct and Reason is not correct explanation of assertion. (C) Assertion is correct and reason is false. (D) assertion is false and reason is correct.
View SolutionHow many geometrical isomers of this compound are possible ?

View SolutionHow many geometrical isomers of this compound are possible:
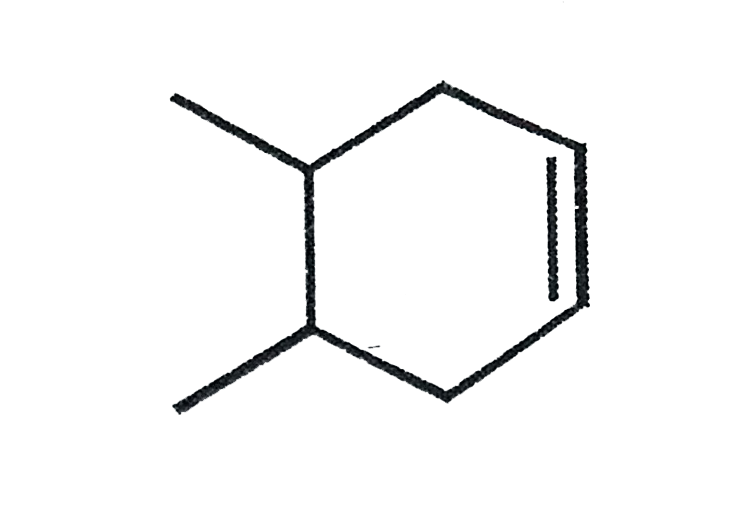
View SolutionHow many geometrical isomers are possible for Hepta-2, 5-dienoic acid:
View SolutionHow many geometrical isomers are possible for MA2B2C2 ?
View SolutionThe second term of an infinte geometric progression is 2 and its sum to infinity is 8. The first term is
View SolutionThe first two terms of a geometric progression add up to 12. The sum of the third and the fourth terms is 48. If the terms of the geometric progression are alternately positive and negative, then the first term is
View Solution