PandQ are two points on a circle of centre C and radius α . The angle PCQ being 2θ , find the value of sinθ when the radius of the circle inscribed in the triangle CPQ is maximum.
To solve the problem, we need to find the value of sinθ when the radius of the circle inscribed in triangle CPQ is maximized. Let's go through the solution step by step.
Step 1: Understanding the Geometry
We have a circle with center C and radius α. Points P and Q lie on the circumference of the circle, forming an angle PCQ=2θ.
Step 2: Area and Semi-perimeter of Triangle CPQ
The area Δ of triangle CPQ can be expressed using the formula:
Δ=12×CP×CQ×sin(2θ)
Since CP=CQ=α (the radius of the circle), we have:
Δ=12×α×α×sin(2θ)=α22sin(2θ)
The semi-perimeter s of triangle CPQ is given by:
s=CP+CQ+PQ2
Using the Law of Cosines, we can find PQ:
PQ2=CP2+CQ2−2⋅CP⋅CQ⋅cos(2θ)=α2+α2−2α2cos(2θ)=2α2(1−cos(2θ))
Thus, PQ=α√2(1−cos(2θ))=α√4sin2(θ)=2αsin(θ).
Now substituting back into the semi-perimeter:
s=α+α+2αsin(θ)2=α(1+sin(θ))
Step 3: Radius of the Inscribed Circle
The radius r of the inscribed circle in triangle CPQ is given by:
r=Δs
Substituting the expressions for Δ and s:
r=α22sin(2θ)α(1+sin(θ))=α2(1+sin(θ))sin(2θ)
Using sin(2θ)=2sin(θ)cos(θ):
r=α2(1+sin(θ))⋅2sin(θ)cos(θ)=αsin(θ)cos(θ)1+sin(θ)
Step 4: Maximizing the Radius
To find the maximum value of r, we differentiate r with respect to θ and set the derivative to zero:
Let f(θ)=sin(θ)cos(θ)1+sin(θ).
Using the quotient rule:
f′(θ)=(1+sin(θ))(cos2(θ)−sin2(θ))−sin(θ)cos(θ)cos(θ)(1+sin(θ))2
Setting the numerator equal to zero:
(1+sin(θ))(cos2(θ)−sin2(θ))−sin(θ)cos2(θ)=0
Step 5: Solving the Equation
This simplifies to:
cos2(θ)+sin(θ)cos2(θ)−sin2(θ)−sin(θ)sin2(θ)=0
Factoring gives:
cos2(θ)(1+sin(θ))−sin2(θ)(1+sin(θ))=0
This leads to:
(1+sin(θ))(cos2(θ)−sin2(θ))=0
Since 1+sin(θ)≠0, we have:
cos2(θ)=sin2(θ)⟹tan2(θ)=1⟹tan(θ)=1⟹θ=π4
Step 6: Finding sinθ
Thus, sinθ=sin(π4)=√22.
Final Answer
sinθ=√22
We have a circle with center C and radius α. Points P and Q lie on the circumference of the circle, forming an angle PCQ=2θ.
The area Δ of triangle CPQ can be expressed using the formula:
Δ=12×CP×CQ×sin(2θ)
Since CP=CQ=α (the radius of the circle), we have:
Δ=12×α×α×sin(2θ)=α22sin(2θ)
s=CP+CQ+PQ2
Using the Law of Cosines, we can find PQ:
PQ2=CP2+CQ2−2⋅CP⋅CQ⋅cos(2θ)=α2+α2−2α2cos(2θ)=2α2(1−cos(2θ))
Thus, PQ=α√2(1−cos(2θ))=α√4sin2(θ)=2αsin(θ).
s=α+α+2αsin(θ)2=α(1+sin(θ))
The radius r of the inscribed circle in triangle CPQ is given by:
r=Δs
Substituting the expressions for Δ and s:
r=α22sin(2θ)α(1+sin(θ))=α2(1+sin(θ))sin(2θ)
Using sin(2θ)=2sin(θ)cos(θ):
r=α2(1+sin(θ))⋅2sin(θ)cos(θ)=αsin(θ)cos(θ)1+sin(θ)
To find the maximum value of r, we differentiate r with respect to θ and set the derivative to zero:
Let f(θ)=sin(θ)cos(θ)1+sin(θ).
f′(θ)=(1+sin(θ))(cos2(θ)−sin2(θ))−sin(θ)cos(θ)cos(θ)(1+sin(θ))2
Setting the numerator equal to zero:
(1+sin(θ))(cos2(θ)−sin2(θ))−sin(θ)cos2(θ)=0
This simplifies to:
cos2(θ)+sin(θ)cos2(θ)−sin2(θ)−sin(θ)sin2(θ)=0
Factoring gives:
cos2(θ)(1+sin(θ))−sin2(θ)(1+sin(θ))=0
This leads to:
(1+sin(θ))(cos2(θ)−sin2(θ))=0
Since 1+sin(θ)≠0, we have:
cos2(θ)=sin2(θ)⟹tan2(θ)=1⟹tan(θ)=1⟹θ=π4
Thus, sinθ=sin(π4)=√22.
sinθ=√22
Similar Questions
In a right angled triangle ABC, right angled at B, BC=12cm and AB=5cm. The radius of the circle inscribed in the triangle (in cm) is :
View SolutionAn isosceles triangle of vertical angle 2θ is inscribed in a circle of radius a . Show that the area of the triangle is maximum when θ=π6 .
View SolutionIf the tangent at a point P to a circle with centre O cuts a line through O at Q such that PQ=24cm and OQ=25cm . Find the radius of the circle.
View SolutionPQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T . Find the length TP .
View SolutionA point P is 13cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12 cm. Find the radius of the circle.
View SolutionMake a point P and draw a circle with centre P and radius 5 cm. Take any point Q on the circle drawn. With Q as centre and radius 3 cm draw another circle. Label the two points at which the circles intersect as A and B. Join PQ and AB. Find the angle between AB and PQ.
View SolutionA circle is inscribed in an equilateral triangle ABC of side 12 cm, touching its sides (Figure). Find the radius of the inscribed circle and the area of the shaded part.
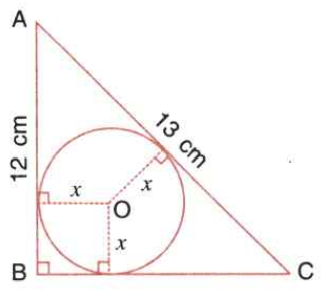
View SolutionABC is a right angled triangle with AB=12 cm and AC=13 cm. A circle, with centre O has been inscribed inside the triangle. Calculate the value of x, the radius of the inscribed circle.
View SolutionDraw a circle of radius 3 cm. Take a point P outside it. Without using the centre of the circle, draw two tangents to the circle from the point P.
View SolutionDraw a circle of radius 3 cm and take a point P outside it. Without using the centre of the circle draw two tangents of the circle from the point P.
View Solution
