PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T . Find the length TP .
To solve the problem, we need to find the length of TP where P and Q are points on the circle, and PQ is a chord of length 8 cm in a circle of radius 5 cm. The tangents at points P and Q intersect at point T.
1. Draw the Circle and Chord:
- Draw a circle with center O and radius 5 cm.
- Mark the chord PQ such that its length is 8 cm.
2. Identify the Midpoint of the Chord:
- Let R be the midpoint of chord PQ. Since PQ=8 cm, then PR=RQ=82=4 cm.
3. Draw the Radius to the Midpoint:
- Draw the radius OR from the center O to the midpoint R. This radius is perpendicular to the chord PQ.
4. Use the Pythagorean Theorem in Triangle OPR:
- In right triangle OPR:
OP2=OR2+PR2
- Here, OP=5 cm (radius), PR=4 cm, and we need to find OR:
52=OR2+42
25=OR2+16
OR2=25−16=9⟹OR=√9=3 cm
5. Find the Length of TP:
- In triangle PTR, where T is the point where the tangents intersect:
- TP2=PR2+RT2
- Let TP=x and RT be the length from R to T. Since TR is perpendicular to OP:
- We can use the Pythagorean theorem again:
TO2=TP2+OP2
- We know TO=TR+OR. Therefore:
TO2=(RT+3)2
- Since TP=x:
x2=42+RT2
x2=16+RT2
6. Use the Relationship Between Tangents:
- Since TP=TQ, we can set up the equation:
(RT+3)2=52+x2
- Substitute x2=16+RT2 into the equation:
(RT+3)2=25+(16+RT2)
(RT+3)2=41+RT2
7. Solve for RT:
- Expanding (RT+3)2:
RT2+6RT+9=41+RT2
6RT+9=41
6RT=32⟹RT=326=163
8. Substitute Back to Find TP:
- Now substitute RT back to find TP:
x2=16+(163)2
x2=16+2569
x2=1449+2569=4009
x=√4009=203
Final Answer:
The length of TP is 203 cm.
- Draw a circle with center O and radius 5 cm.
- Mark the chord PQ such that its length is 8 cm.
- Let R be the midpoint of chord PQ. Since PQ=8 cm, then PR=RQ=82=4 cm.
- Draw the radius OR from the center O to the midpoint R. This radius is perpendicular to the chord PQ.
- In right triangle OPR:
OP2=OR2+PR2
- Here, OP=5 cm (radius), PR=4 cm, and we need to find OR:
52=OR2+42
25=OR2+16
OR2=25−16=9⟹OR=√9=3 cm
- In triangle PTR, where T is the point where the tangents intersect:
- TP2=PR2+RT2
- Let TP=x and RT be the length from R to T. Since TR is perpendicular to OP:
- We can use the Pythagorean theorem again:
TO2=TP2+OP2
- We know TO=TR+OR. Therefore:
TO2=(RT+3)2
- Since TP=x:
x2=42+RT2
x2=16+RT2
- Since TP=TQ, we can set up the equation:
(RT+3)2=52+x2
- Substitute x2=16+RT2 into the equation:
(RT+3)2=25+(16+RT2)
(RT+3)2=41+RT2
- Expanding (RT+3)2:
RT2+6RT+9=41+RT2
6RT+9=41
6RT=32⟹RT=326=163
- Now substitute RT back to find TP:
x2=16+(163)2
x2=16+2569
x2=1449+2569=4009
x=√4009=203
The length of TP is 203 cm.
Topper's Solved these Questions
Similar Questions
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (see Fig. 10.10). Find the length TP.
View SolutionAB is a chord of length 16cm of a circle of radius 10cm. The tangents at A and B intersect at a point P . Find the length of PA .
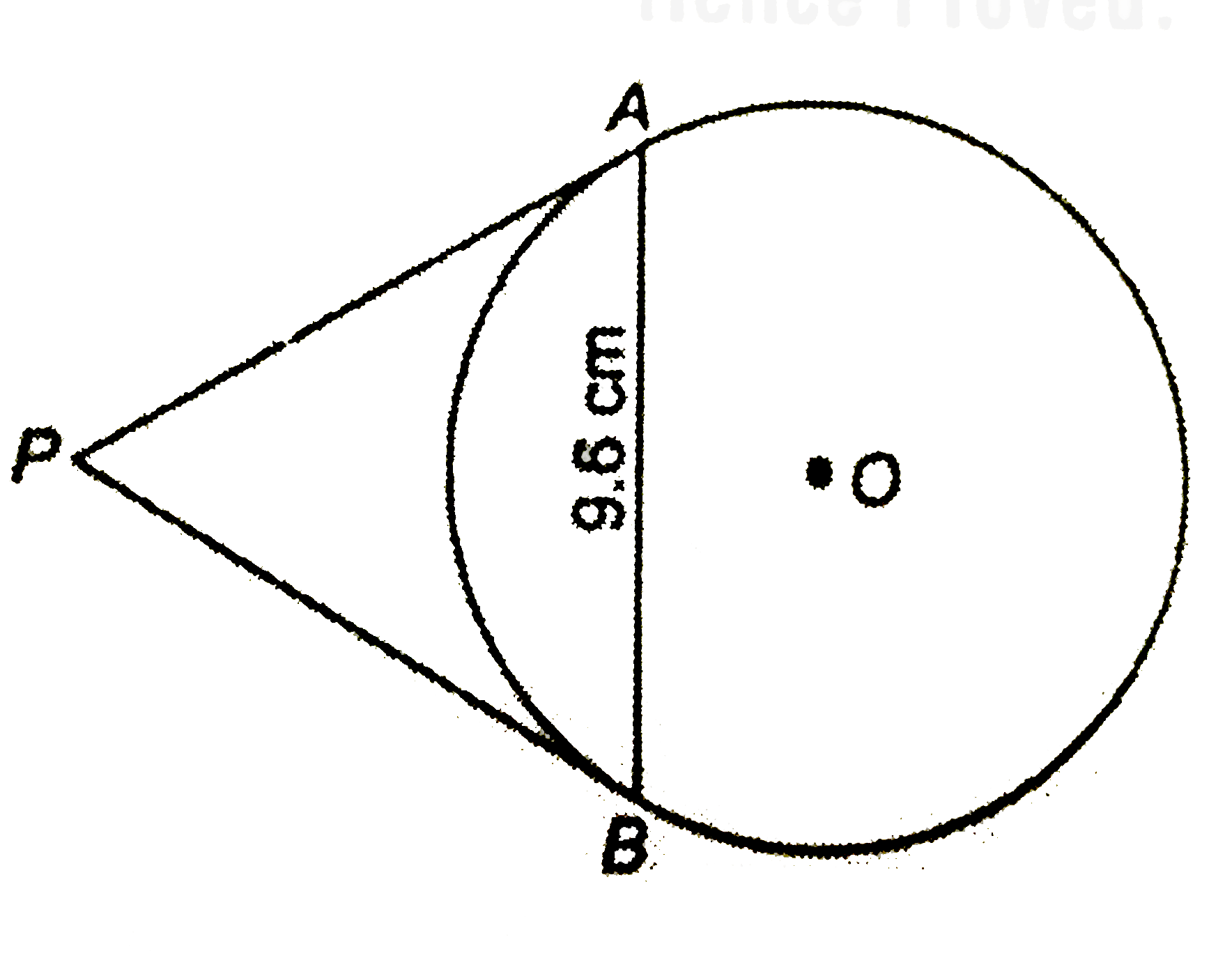
View SolutionIn the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.
View SolutionDraw a circle of radius 3.0 cm. Take a point P on it. Construct a tangent at point P.
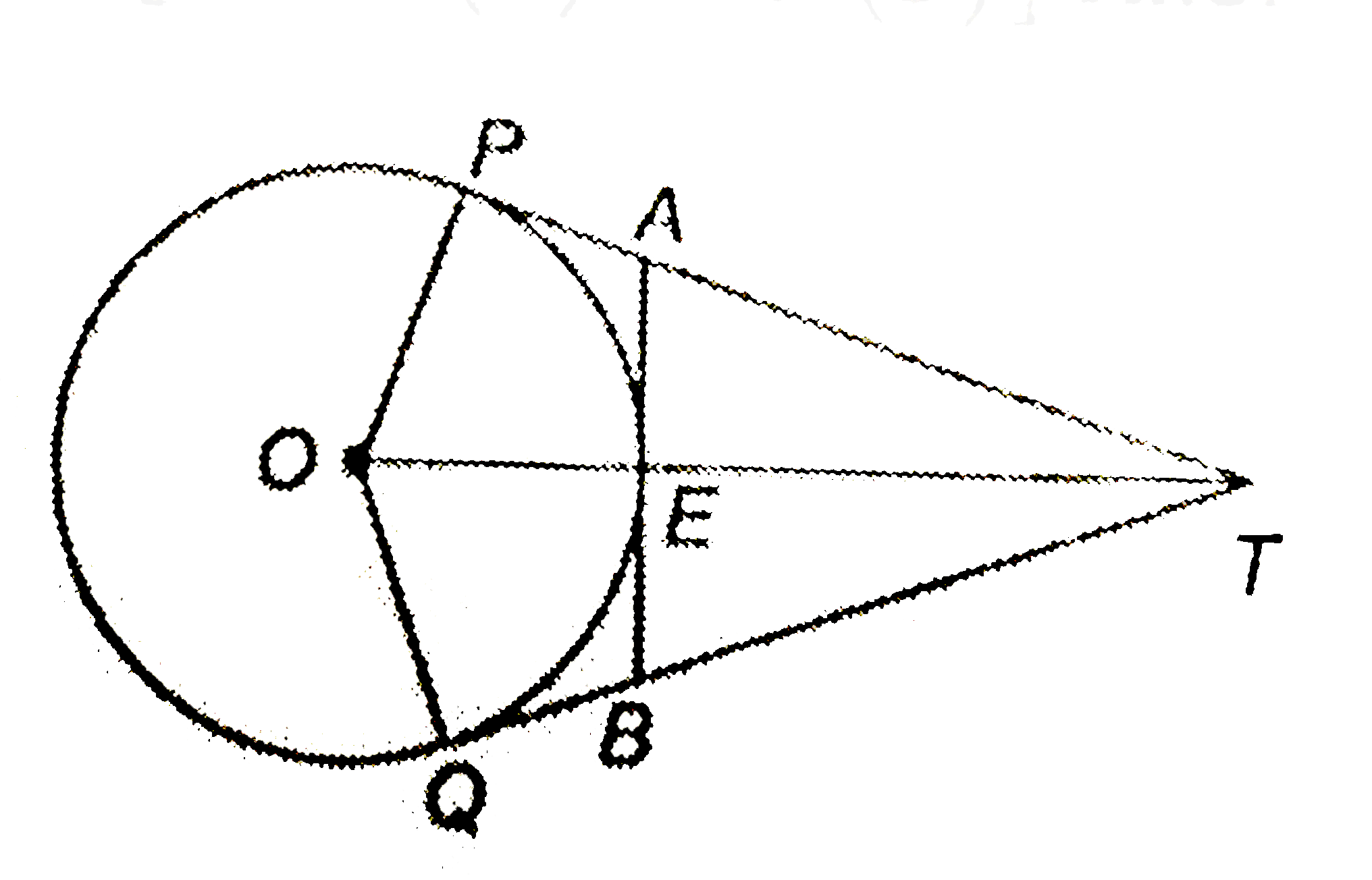
View SolutionO is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E, find the length AB.
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ=13cm . Find the length of PQ .
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ=12cm. Length PQ is :
(A) 12 cm (B) 13 cm (C) 8.5 cm (D) √119cm.
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q such that OQ=12cm . Length PQ is
View SolutionTwo circles intersect each other at points A and B. A straight line PAQ cuts the circles at P and Q. If the tangents at P and Q intersect at point T, show that the points P, B, Q and T are concylic.
View SolutionA line through the centre O of a circle of radius 7 cm cuts the tangent, at a point P on the circle, at Q such that PQ=24cm . Find OQ .
View Solution
