Two points P(a,0) and Q(-a,0) are given. R is a variable point on one side of the line PQ such that ∠RPQ−∠RQP is a positive constant 2α. Find the locus of the point R.
To find the locus of the point R given the points P(a,0) and Q(−a,0), and the condition that the difference between the angles ∠RPQ and ∠RQP is a positive constant 2α, we can follow these steps:
Step 1: Define the Coordinates
Let the coordinates of point R be R(x,y). The coordinates of points P and Q are given as P(a,0) and Q(−a,0).
Step 2: Use the Angle Condition
According to the problem, we have:
∠RPQ−∠RQP=2α
This can be rewritten using the tangent of the angles:
tan(∠RPQ)−tan(∠RQP)=tan(2α)
Step 3: Express the Tangents
Using the coordinates, we can express the tangents of the angles:
- For ∠RPQ:
tan(∠RPQ)=yx−a
- For ∠RQP:
tan(∠RQP)=yx+a
Step 4: Substitute into the Equation
Substituting these into the angle condition gives:
yx−a−yx+a=tan(2α)
Step 5: Simplify the Expression
Combining the left-hand side:
y((x+a)−(x−a))(x−a)(x+a)=y(2a)x2−a2
Thus, we have:
2ayx2−a2=tan(2α)
Step 6: Rearranging the Equation
Rearranging gives:
2ay=(x2−a2)tan(2α)
Step 7: Final Locus Equation
This can be rearranged to find the locus of point R:
y=(x2−a2)tan(2α)2a
Step 8: Identify the Locus
This equation represents a parabola in the xy-plane.
Final Answer
The locus of the point R is given by:
y=tan(2α)2a(x2−a2)
---
Let the coordinates of point R be R(x,y). The coordinates of points P and Q are given as P(a,0) and Q(−a,0).
According to the problem, we have:
∠RPQ−∠RQP=2α
This can be rewritten using the tangent of the angles:
tan(∠RPQ)−tan(∠RQP)=tan(2α)
Using the coordinates, we can express the tangents of the angles:
- For ∠RPQ:
tan(∠RPQ)=yx−a
- For ∠RQP:
tan(∠RQP)=yx+a
Substituting these into the angle condition gives:
yx−a−yx+a=tan(2α)
Combining the left-hand side:
y((x+a)−(x−a))(x−a)(x+a)=y(2a)x2−a2
Thus, we have:
2ayx2−a2=tan(2α)
Rearranging gives:
2ay=(x2−a2)tan(2α)
This can be rearranged to find the locus of point R:
y=(x2−a2)tan(2α)2a
This equation represents a parabola in the xy-plane.
The locus of the point R is given by:
y=tan(2α)2a(x2−a2)
Topper's Solved these Questions
Similar Questions
Given P=(1,0) and Q=(−1,0) and R is a variable point on one side of the line PQ such that ∠RPQ−∠RQP=π4. The locus of the point R is
View SolutionS and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
View SolutionIn PQR , S is any point on the side QR . Show that PQ+QR+RP>2PS
View SolutionGiven that P(3,1),Q(6.5), and R(x,y) are three points such that the angle PRQ is a right angle and the area of RQP is 7, find the number of such points R.
View SolutionIf P,Q and R are three collinear points such that →PQ=→a and →QR = →b. Find the vector →PR .
View SolutionGiven points P(2,3),Q(4,−2),andR(α,0). Find the value of a if PR+RQ is minimum.
View SolutionIn Figure, T is a point on side QR of PQR and S is a point such that RT=ST. Prove That : PQ+PR>QS
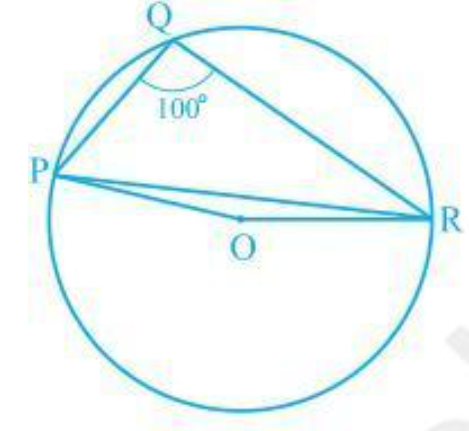
View Solution∠PQR=100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR
View SolutionShow that the relation R on the set A of points in a plane, given by R={(P, Q): Distance of the point P from the origin is same as the distance of the point Q from the origin}, is an equivalence relation. Further show that the set of all points related to a point P≠(0, 0) is the circle passing through P with origin as centre.
View SolutionShow that the relation R on the set A of points in a plane, given by R={(P, Q): Distance of the point P from the origin is same as the distance of the point Q from the origin}, is an equivalence relation. Further show that the set of all points related to a point P≠(0, 0) is the circle passing through P with origin as centre.
View Solution
