$∠ P Q R = 100^{\circ}$ , where P, Q and R are points on a circle with centre O. Find $∠ O P R$

Video Solution

Text Solution

Verified by Experts

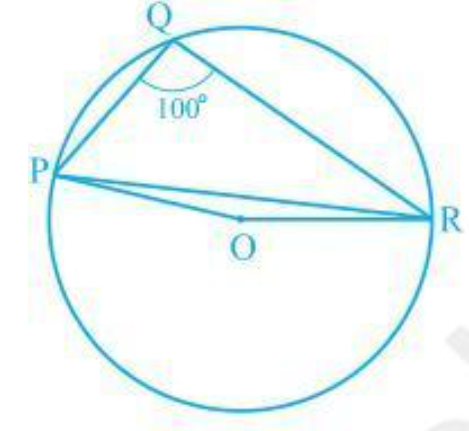
Since all points $P, Q, R, S$ lie on the circle, $P Q R S$ becomes a cyclic quadrilateral.
We know that the sum of either pair of opposite angles of a cyclic quadrilateral is $180^{\circ}$
Therefore, $∠ P Q R + ∠ P S R = 180^{\circ}$
$100^{\circ} + ∠ P S R = 180^{\circ}$
$∠ P S R = 180^{\circ} - 100^{\circ} = 80^{\circ}$
We know that the angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle
Therefore, $∠ P O R = 2 ∠ P S R$
= $2 \times 80^{\circ}$
= $160^{\circ}$
Consider the $△ O P R$ . It is an isosceles triangle as $O P = O R$ = Radius of the circle.
Thus, $∠ O P R = ∠ O R P$
Sum of all angles in a triangle is $180^{\circ}$
Therefore, $∠ O P R + ∠ P O R + ∠ O R P = 180^{\circ}$
$∠ O P R + 160^{\circ} + ∠ O P R = 180^{\circ}$
$2 ∠ O P R = 180^{\circ} - 160^{\circ}$
$∠ O P R = 10^{\circ}$

|

Updated on:21/07/2023

Class 9 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

NCERT ENGLISH-CIRCLES-EXERCISE 10.5

Home
Ask Doubt
Profile