Each equation contains statements given in two columns which have to be matched. Statements (a,b,c,d) in column I have to be matched with Statements (p, q, r, s) in column II. If the correct match are a→p,a→s,b→q,b→r,c→p,c→q, and d→s , then the correctly bubbled 4x4 matrix should be as follows: Figure Consider the lines represented by equation (x2+xy−x)x(x−y)=0, forming a triangle. Then match the following: Column I|Column II Orthocenter of triangle |p. (16,12) Circumcenter|q. (1(2+2√2),12) Centroid|r. (0,12) Incenter|s. (12,12)
To solve the problem, we need to match the statements in Column I with those in Column II based on the properties of the triangle formed by the given lines. Let's break down the steps:
Step 1: Analyze the Given Equation
The equation provided is:
(x2+xy−x)(x−y)=0
This equation can be factored into two parts:
1. x2+xy−x=0
2. x−y=0
Step 2: Solve the First Part
For the first part x2+xy−x=0:
- Rearranging gives x2+xy−x=0.
- Factoring out x gives x(x+y−1)=0.
- This results in two equations:
- x=0
- x+y−1=0 or y=1−x
Step 3: Solve the Second Part
The second part x−y=0 gives:
- y=x
Step 4: Identify the Lines
From the above, we have the following lines:
1. x=0 (the y-axis)
2. y=1−x (a line with a negative slope intersecting the y-axis at 1)
3. y=x (a line with a positive slope through the origin)
Step 5: Find the Intersection Points
To find the vertices of the triangle formed by these lines:
- Point A (intersection of x=0 and y=1−x):
- Set x=0 in y=1−x gives y=1.
- So, A(0,1).
- Point B (intersection of x=0 and y=x):
- Set x=0 gives y=0.
- So, B(0,0).
- Point C (intersection of y=1−x and y=x):
- Set 1−x=x gives 2x=1 or x=12.
- Substitute x=12 into y=x gives y=12.
- So, C(12,12).
Step 6: Find Centroid, Orthocenter, Circumcenter, and Incenter
1. Centroid (G):
G(x1+x2+x33,y1+y2+y33)=⎛⎝0+0+123,1+0+123⎞⎠=(16,12)
2. Orthocenter (H):
For right triangles, the orthocenter is at the vertex opposite the hypotenuse. Here, it is at point C(12,12).
3. Circumcenter (O):
The circumcenter is the midpoint of the hypotenuse in a right triangle. The hypotenuse is AB:
O(0+02,1+02)=(0,12)
4. Incenter (I):
The incenter is the intersection of the angle bisectors. For this triangle, it can be calculated as:
I(12,12)
Step 7: Match the Points
Now we can match the points with the statements in Column II:
- Orthocenter H matches with p (16,12)
- Circumcenter O matches with q (1(2+2√2),12)
- Centroid G matches with r (0,12)
- Incenter I matches with s (12,12)
Final Matches
- a→p
- b→q
- c→r
- d→s
The equation provided is:
(x2+xy−x)(x−y)=0
This equation can be factored into two parts:
1. x2+xy−x=0
2. x−y=0
For the first part x2+xy−x=0:
- Rearranging gives x2+xy−x=0.
- Factoring out x gives x(x+y−1)=0.
- This results in two equations:
- x=0
- x+y−1=0 or y=1−x
The second part x−y=0 gives:
- y=x
From the above, we have the following lines:
1. x=0 (the y-axis)
2. y=1−x (a line with a negative slope intersecting the y-axis at 1)
3. y=x (a line with a positive slope through the origin)
To find the vertices of the triangle formed by these lines:
- Point A (intersection of x=0 and y=1−x):
- Set x=0 in y=1−x gives y=1.
- So, A(0,1).
- Set x=0 gives y=0.
- So, B(0,0).
- Set 1−x=x gives 2x=1 or x=12.
- Substitute x=12 into y=x gives y=12.
- So, C(12,12).
1. Centroid (G):
G(x1+x2+x33,y1+y2+y33)=⎛⎝0+0+123,1+0+123⎞⎠=(16,12)
For right triangles, the orthocenter is at the vertex opposite the hypotenuse. Here, it is at point C(12,12).
The circumcenter is the midpoint of the hypotenuse in a right triangle. The hypotenuse is AB:
O(0+02,1+02)=(0,12)
The incenter is the intersection of the angle bisectors. For this triangle, it can be calculated as:
I(12,12)
Now we can match the points with the statements in Column II:
- Orthocenter H matches with p (16,12)
- Circumcenter O matches with q (1(2+2√2),12)
- Centroid G matches with r (0,12)
- Incenter I matches with s (12,12)
- a→p
- b→q
- c→r
- d→s
Topper's Solved these Questions
Similar Questions
Each question contains statements given in two columns which have to be matched . Statement (A,B,C,D) in column I have to be matched statements (p,q,r,s) in column II. Capillary rise and shape of droplets on a plate due to surface tension are shown in column - II . Match the following

View SolutionEach question contains statements given in two columns which have to be matched . Statement (A,B,C,D) in column I have to be matched statements (p,q,r,s) in column II. Capillary rise and shape of droplets on a plate due to surface tension are shown in column - II . Match the following

View SolutionMatch the statements (A, B, C, D) in Column I with the statements (p, q, r, s) in column II. The answers are to be properly bubbled.
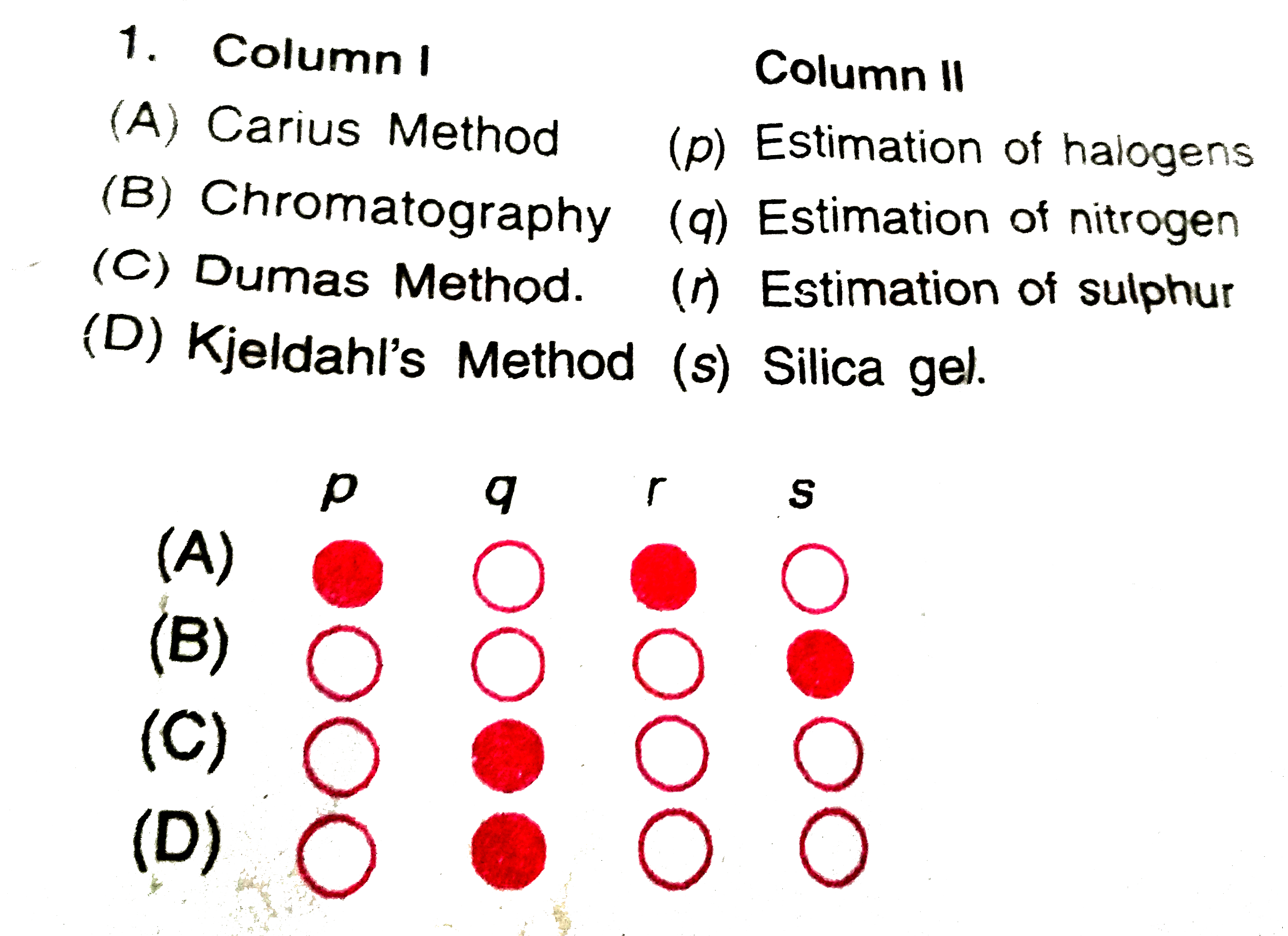
View SolutionMatch the statement (A, B, C, D) in Column I with the statements (p, q, r, s) in Column II. The answer are to be properly bubbled.

View SolutionMatch the statement (A, B, C, D) in Column I with the statements (p, q, r, s) in Column II. The answer are to be properly bubbled.

View SolutionMatch the statement (A, B, C, D) in Column I with the statements (p, q, r, s) in Column II. The answer are to be properly bubbled.

View SolutionMatch the statement (A, B, C, D) in Column I with the statements (p, q, r, s) in Column II. The answer are to be properly bubbled.

View SolutionMatch the statement (A,B,C,D) in column I with the statement (p,q,r,s) in column II. The answers are to be properly bobbled.
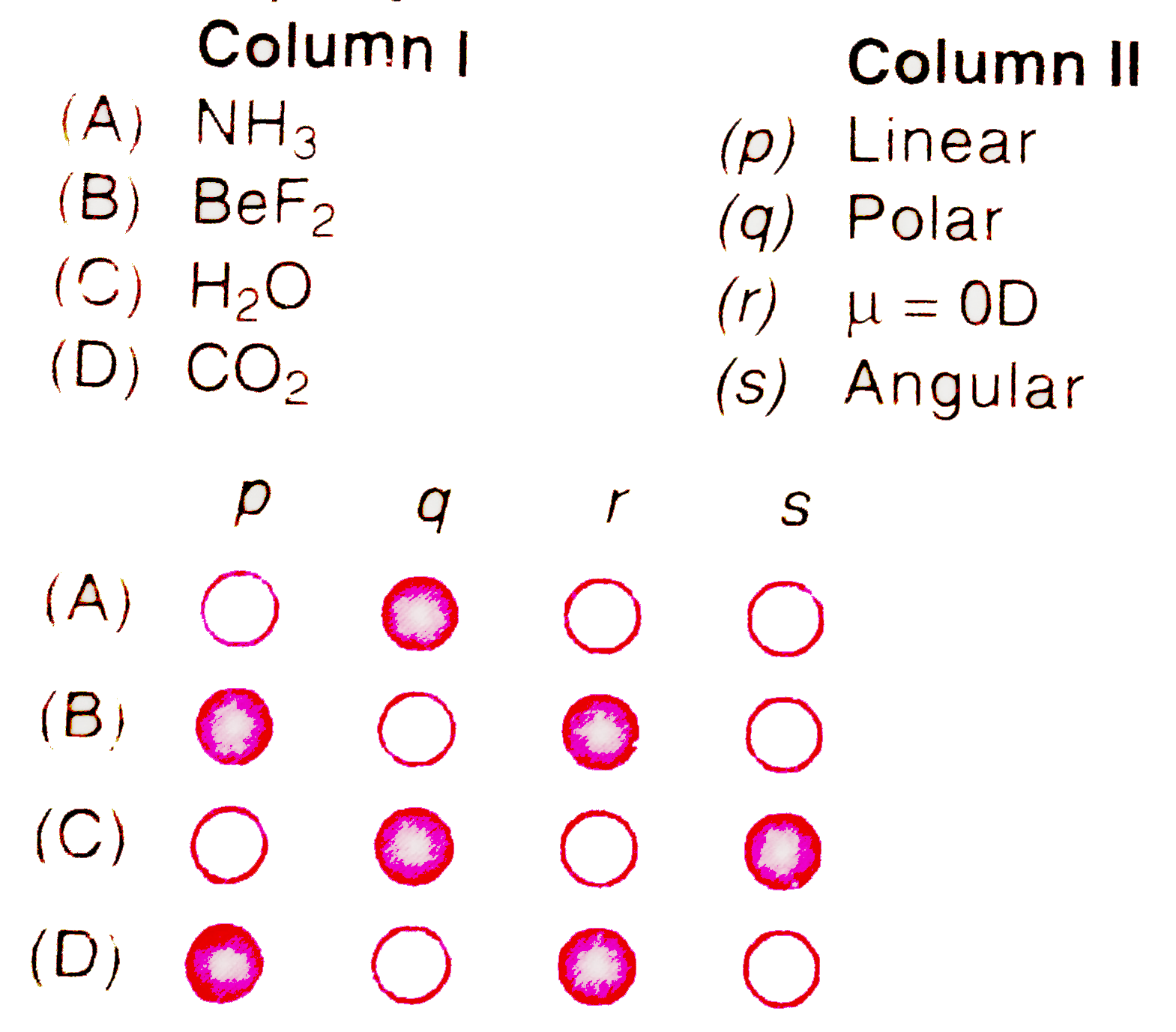
View SolutionEach question contains statements given in two columns which have to be matched. Statements a,b,c,d in column I have to be matched with statements p,q,r,s in column II. If the correct matches are a-p, q-s, b-q, r c-p, q and d-s, then the correctly bubbled 4x4 matrix should be as follows: Figure Column I, Column II: Differential equation order 1, p. of all parabolas whose axis is the x-axis order 2, q. of family of curves y=a(x+a)2, whre a is an arbitrary constant degree 1, r. (1+3dydx)23=4d3ydx3 degree 3, s. of family of curve y2=2c(x+√c), where c>0
View SolutionEach question contains statements given in two columns which have to be matched. Statements (a,b,c,d) in column I have to be matched with statements (p,q,r,s) in column II. If the correct match are a-p, s, b-r c-p, q. and d-s, then the correctly bubbled 4x4 matrix should be as follows: figure Column I, a) If ∫2x√1−4xdx=ksin−1(f(x))+C, then kis greater than, b) If ∫(√x)5(√x)7+x6dx=aln(xk)xk+1+c, then akis less than, c) If ∫x4+1x(x2+1)2dx=kln|x|+m1+x2+n, where nis the constant of integration, then mkis greater than, d) If ∫dx5+4cosx=ktan−1(mtanx2)+C, then k/mis greater than, COLUMN II p) 0 q) 1 r) 3 s)4
View Solution
