The ends of a quadrant of a circle have the coordinates (1, 3) and (3, 1). Then the center of such a circle is
To find the center of the circle whose ends of a quadrant are given by the coordinates (1, 3) and (3, 1), we can follow these steps:
Step 1: Identify the points
Let the points be A(1,3) and B(3,1).
Step 2: Find the midpoint of line segment AB
The center of the circle will lie on the line segment joining points A and B. We can find the midpoint M of segment AB using the midpoint formula:
M=(x1+x22,y1+y22)
Substituting the coordinates of points A and B:
M=(1+32,3+12)=(42,42)=(2,2)
Step 3: Find the slope of line segment AB
The slope m of line segment AB can be calculated using the formula:
m=y2−y1x2−x1
Substituting the coordinates of points A and B:
m=1−33−1=−22=−1
Step 4: Find the slope of the perpendicular bisector
The slope of the perpendicular bisector will be the negative reciprocal of the slope of line segment AB. Thus:
mperpendicular=−1m=−1−1=1
Step 5: Write the equation of the perpendicular bisector
Using point-slope form of the equation of a line, the equation of the perpendicular bisector passing through point M(2,2) is:
y−y1=m(x−x1)
Substituting the midpoint and the slope:
y−2=1(x−2)
Simplifying this gives:
y−2=x−2⟹y=x
Step 6: Find the intersection of the perpendicular bisector with the line y = x
Since the center of the circle must lie on the line y=x, we can substitute y in the coordinates of points A and B to find the center.
Step 7: Calculate the center
Since the center must also be equidistant from both points A and B, we can directly check the coordinates along the line y=x. The center will be at the point where x=y and lies between the coordinates of points A and B.
The center of the circle is:
C(2,2)
Final Answer
Thus, the center of the circle is (2,2).
---
Let the points be A(1,3) and B(3,1).
The center of the circle will lie on the line segment joining points A and B. We can find the midpoint M of segment AB using the midpoint formula:
M=(x1+x22,y1+y22)
Substituting the coordinates of points A and B:
M=(1+32,3+12)=(42,42)=(2,2)
The slope m of line segment AB can be calculated using the formula:
m=y2−y1x2−x1
Substituting the coordinates of points A and B:
m=1−33−1=−22=−1
The slope of the perpendicular bisector will be the negative reciprocal of the slope of line segment AB. Thus:
mperpendicular=−1m=−1−1=1
Using point-slope form of the equation of a line, the equation of the perpendicular bisector passing through point M(2,2) is:
y−y1=m(x−x1)
Substituting the midpoint and the slope:
y−2=1(x−2)
Simplifying this gives:
y−2=x−2⟹y=x
Since the center of the circle must lie on the line y=x, we can substitute y in the coordinates of points A and B to find the center.
Since the center must also be equidistant from both points A and B, we can directly check the coordinates along the line y=x. The center will be at the point where x=y and lies between the coordinates of points A and B.
C(2,2)
Thus, the center of the circle is (2,2).
Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
886 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
Knowledge Check
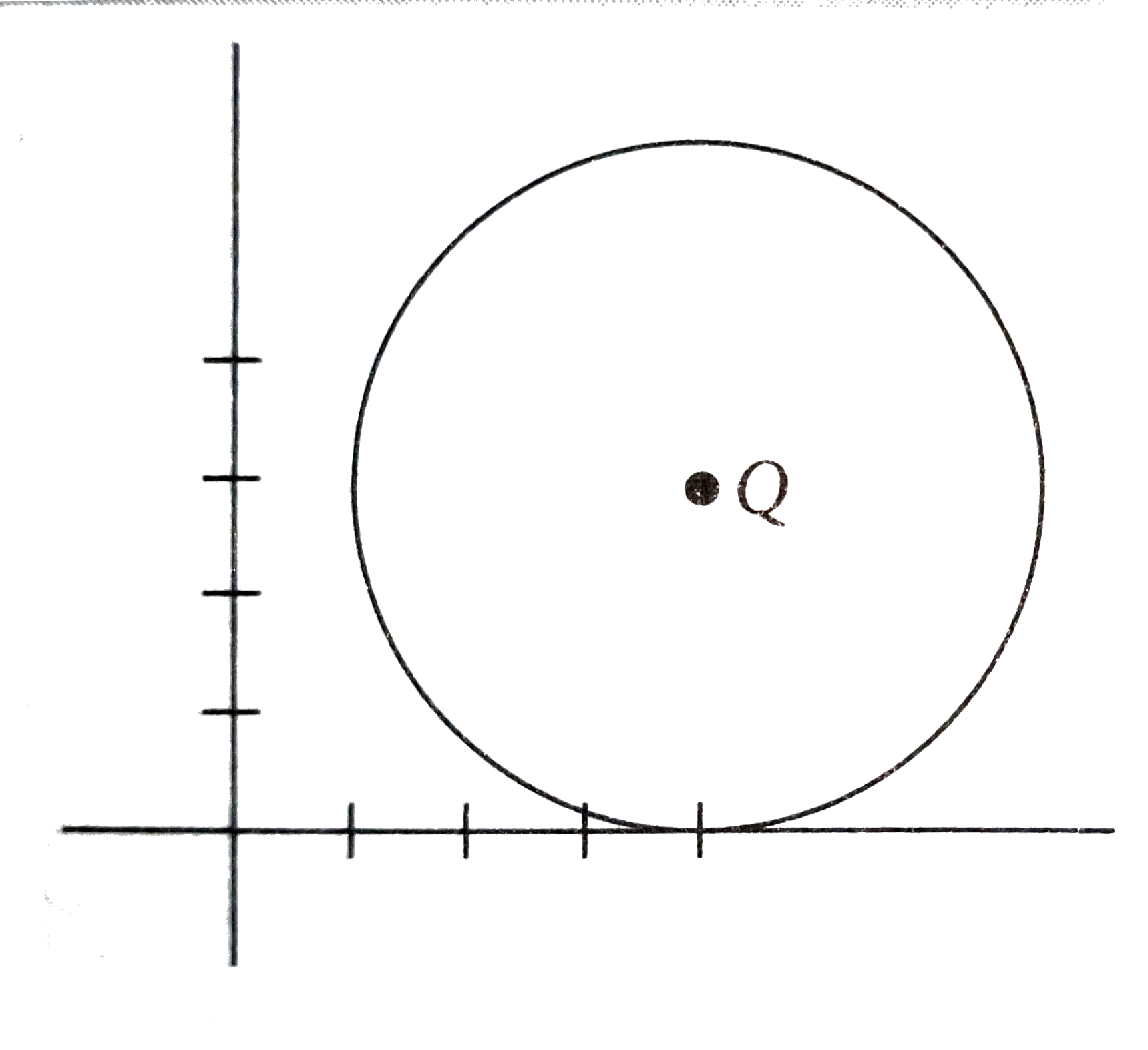
Center Q of the circle above has coordinate of (4,3). What is the circumference of the circle?AπB2πC6πD9π
Point K is the center of the circle above, and the coordinates of Point K are (2, -1). What is the area of the circle?AπB2πC4πD8π
The endpoints of a diameter of a circle are (3,1) and (3,5) then equation of the circle is
View SolutionThe coordinates of one end point of a diameter of a circle are (4,−1) and the coordinates of the centre of the circle are (1,−3) . Find the coordinates of the other end of the diameter.
View SolutionLine 2x+3y+1=0 is a tangent to the circle at (1,-1). This circle is orthogonal to a circle which is drawn having diameter as a line segment with end points (0, -1) and (-2, 3). Then the equation of the circle is
View SolutionA circle touches the x-axis and also thouches the circle with center (0, 3) and radius 2. The locus of the center of the circle is (a) a circle (b) an ellipse (c) a parabola (d) a hyperbola
View SolutionFind the equation of the circle if the chord of the circle joining (1, 2) and (−3,1) subtents 900 at the center of the circle.
View SolutionThe coordinates of one end of a diameter of a circle are (5,−7). If the coordinates of the centre be (7,3) find the coordinates of the other end of the diameter.
View Solution
