A lift of mass m is supported by a cable that can with stand a force of 3mg. Find the shortest distance in which the lift can be stopped when it is descending with a speed of g/4.
The correct Answer is:g/32
To solve the problem, we will follow these steps:
Step 1: Analyze the Forces Acting on the Lift
The lift of mass m is descending with a speed of g4. The forces acting on the lift are:
- The weight of the lift acting downwards: mg
- The tension in the cable acting upwards: T
The cable can withstand a maximum tension of 3mg.
Step 2: Apply Newton's Second Law
Since the lift is descending, we can apply Newton's second law:
T−mg=−ma
Here, a is the upward acceleration (deceleration in the context of stopping the lift).
Step 3: Determine Maximum Tension
Given that the maximum tension T can be 3mg, we substitute this into our equation:
3mg−mg=−ma
This simplifies to:
2mg=−ma
Rearranging gives:
a=−2g
This means the lift is decelerating at 2g upwards.
Step 4: Use Kinematic Equation to Find Distance
We need to find the shortest distance s in which the lift can be stopped. We can use the kinematic equation:
v2=u2+2as
Where:
- v=0 (final velocity when stopped)
- u=g4 (initial velocity)
- a=−2g (deceleration)
Substituting the values into the equation:
0=(g4)2+2(−2g)s
This simplifies to:
0=g216−4gs
Rearranging gives:
4gs=g216
Dividing both sides by g (assuming g≠0):
4s=g16
Thus:
s=g64
Final Answer
The shortest distance in which the lift can be stopped is:
s=g64
---
The lift of mass m is descending with a speed of g4. The forces acting on the lift are:
- The weight of the lift acting downwards: mg
- The tension in the cable acting upwards: T
Since the lift is descending, we can apply Newton's second law:
T−mg=−ma
Here, a is the upward acceleration (deceleration in the context of stopping the lift).
Given that the maximum tension T can be 3mg, we substitute this into our equation:
3mg−mg=−ma
This simplifies to:
2mg=−ma
Rearranging gives:
a=−2g
This means the lift is decelerating at 2g upwards.
We need to find the shortest distance s in which the lift can be stopped. We can use the kinematic equation:
v2=u2+2as
Where:
- v=0 (final velocity when stopped)
- u=g4 (initial velocity)
- a=−2g (deceleration)
0=(g4)2+2(−2g)s
This simplifies to:
0=g216−4gs
Rearranging gives:
4gs=g216
Dividing both sides by g (assuming g≠0):
4s=g16
Thus:
s=g64
The shortest distance in which the lift can be stopped is:
s=g64
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWER
5 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - Problem
162 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - NUMERICAL EXERCISE ( LEVEL-1)
16 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
A 1000 kg lift is supported by a cable that can support 2000 kg. The shortest distance in which the lift can be stopped when it is descending with a speed of 2.5m/s is (g=10m/s2)
View SolutionA driver having a definite reaction time is capable of stopping his car over a distance of 30 m on seeing a red traffic signal, when the speed of the car is 72 km/hr andover a distance of 10 m when the speed is 36 km/hr. Find the distance over which he can stop the car if it were running at a speed of 54 km/hr. Assume that his reaction time and the deceleration of the car remains same in all the three cases.
View Solution
Knowledge Check
A car can be stopped within a distance of s when its speed is v. What is the minimum distance within which the car can be stopped during the same time when its speed is nv ?
AnsBs/nCn2sDs/n2
A man of mass 60 kg records his weight on a weighing machine placed inside a lift . The ratio of the weights of the man recorded when the lift is ascending up with a uniform speed of 2 m/s to when it is descending down with a uniform speed of 4 m/s will be
View SolutionConsider a car moving on a straight road with a speed of 100m/s. The distance at which car can be stopped is [μk=0.5]
View SolutionConsider a car moving on a straight road with a speed of 100m/s. The distance at which car can be stopped is [μk=0.5]
View SolutionA man of mass 60 kg records his wt. on a weighing machine placed inside a lift. The ratio of wts. Of man recorded when lift is ascending up with a uniform speed of 2 m/s to when it is descending down with a uniform speed of 4 m/s will be
View SolutionA uniform horizontal beam of length L and mass M is attached to a wall by a pin connection. Its far end is supported by a cable that makes an angle θ with the horizontal . If a man of mass 'm' stands at a distance l from the wall , find the tension in the cable in equilibrium.
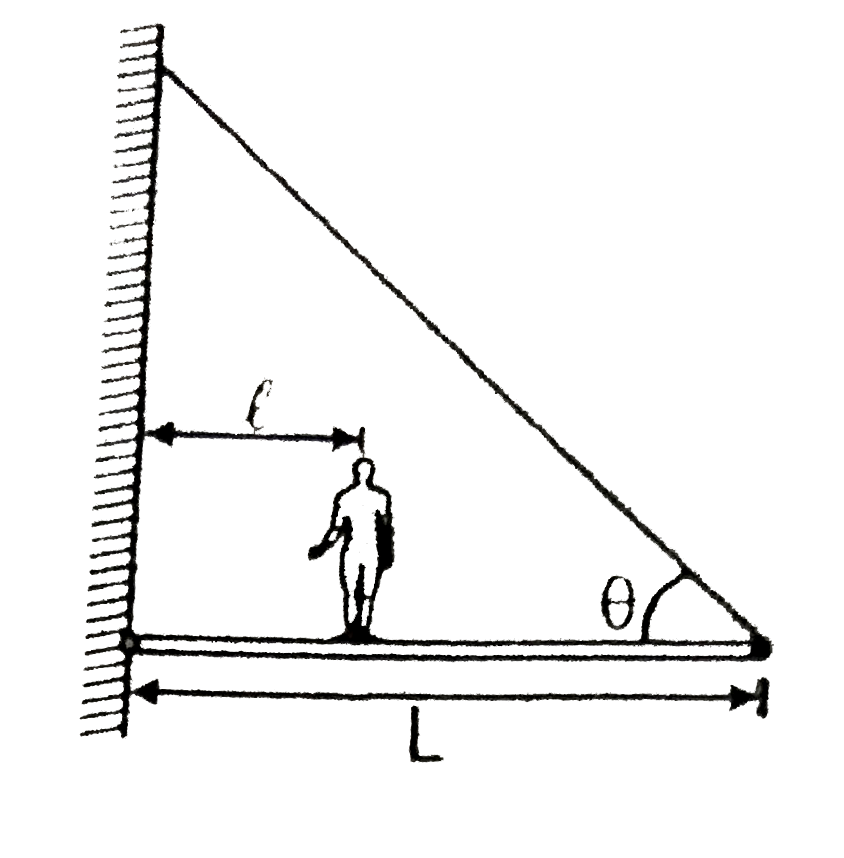
View SolutionThe cable of a uniformly loaded suspension bridge hangs in the form of a parabola. The roadway which is horizontal and 100m long is supported by vertical wires attached to the cable, the longest wire being 30m and the shortest being 6m. Find the length of the supporting wire attached to the roadway 18m from the middle.
View SolutionA man of mass m is standing on a lift which moves down with an upward acceleration a. Find the pseudo force acting on the man as observed by himself. Find the pseudo force acting on the man if the lift falls freely.
View Solution
