If the standard deviation of a variable ξsσ , then standard deviation of variable aX+bc is aσ (b) acσ (c) ∣∣ac∣∣σ (d) aσ+bc
(ac)σ
∣∣ac∣∣σ
(a2c2)σ
None of these
The correct Answer is:B
Let y=αx+bc,i.e.,y=acx+bc
i.e., y=acx+bc
∴¯y=A¯x+B
∴y−¯y=A(x−¯x)
⇒(y−¯y)2=A2(x−¯x)2
⇒∑(y−¯y)2=A2∑(x−¯x)2
⇒n.σ2y=A2.nσ2x
⇒σ2y=A2σ2x
⇒σy=|A|σx
⇒σy=∣∣ac∣∣σx
Thus, new SD =∣∣ac∣∣σ
Topper's Solved these Questions
- STATISTICSBOOK - CENGAGE ENGLISHCHAPTER - STATISTICSEXERCISE - Archives
10 Videos
- STATISTICSBOOK - CENGAGE ENGLISHCHAPTER - STATISTICSEXERCISE - Exercise 11.2
6 Videos
- SOLUTIONS AND PROPERTIES OF TRIANGLE BOOK - CENGAGE ENGLISHCHAPTER - SOLUTIONS AND PROPERTIES OF TRIANGLE EXERCISE - Comprehension Type
6 Videos
- STRAIGHT LINEBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
Similar Questions
Knowledge Check
Let x1,x2,x3,……..,xn be n observations with mean ¯x and standard deviation σ. The mean the standard deviation of kx1,kx2,……,kxn respectively are
(i) ¯x,kσ
(ii) k¯x,σ
(iii) k¯x,kσ
(iv) ¯x,σA¯x,kσBk¯x,σCk¯x,kσD¯x,σGiven r=√34,byx=12, variance of x=12, then standard deviation of y is
A2B3C4D9
For the following probability distribution determine standard deviation of the random variable X.
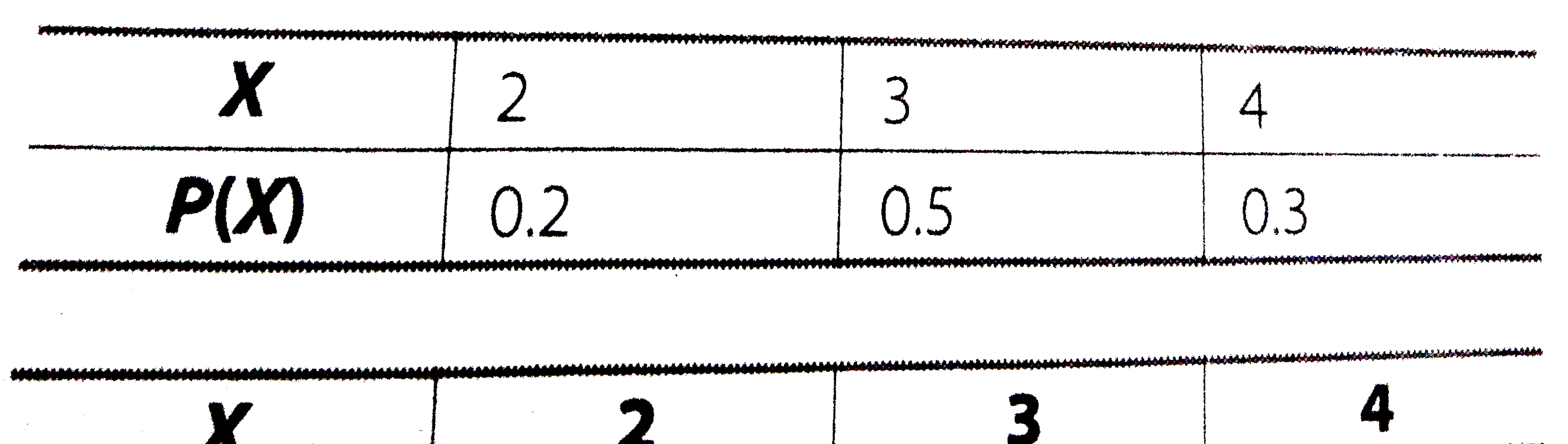
View SolutionLet a, b, c, d, e, be the observations with m and standard deviation s. The standard deviation of the observations a+k, b+k, c+k, d+k, e+k is (a) s (b) ks (c) s+k (d) sk
View SolutionLet a, b, c, d, e, be the observations with m and standard deviation s. The standard deviation of the observations a+k, b+k, c+k, d+k, e+k is s (b) ks (c) s+k (d) sk
View SolutionThe standard deviation of first 10 natural numbers is (a) 8.25 (b) 6.5 (c) 3.87 (d) 2.87
View SolutionThe standard deviation of first 10 natural numbers is (a) 8.25 (b) 6.5 (c) 3.87 (d) 2.87
View SolutionThe standard deviation of first 10 natural numbers is
a) 8.25
(b) 6.5
(c) 3.87
(d) 2.87
View Solution
