If the standard deviation of a variable , then standard deviation of variable is (a) (b) (c) (d)
To find the standard deviation of the variable (aX+b)/c given that the standard deviation of X is σ, we can follow these steps:
Step 1: Understand the transformation
We are transforming the variable X using the formula (aX+b)/c. This transformation involves multiplying X by a, adding b, and then dividing by c.
Hint: Remember that standard deviation is affected by multiplication and division but not by addition or subtraction.
Step 2: Identify the effect of multiplication and division
When we multiply a variable by a constant a, the standard deviation is also multiplied by the absolute value of that constant. Thus, the standard deviation of aX will be |a|σ.
Hint: The formula for standard deviation when multiplying by a constant is SD(aX)=|a|⋅SD(X).
Step 3: Consider the division by c
Next, when we divide by c, the standard deviation is divided by the absolute value of c. Therefore, the standard deviation of (aX)/c will be |a|σ/|c|.
Hint: The formula for standard deviation when dividing by a constant is SD(X/c)=SD(X)/|c|.
Step 4: Combine the transformations
Now, we combine the effects of multiplying by a and dividing by c:
SD(aXc)=|a||c|⋅σ
Hint: When combining transformations, apply the effects sequentially.
Step 5: Adding b
Adding b to the variable does not affect the standard deviation. The standard deviation remains the same after adding or subtracting a constant.
Hint: Standard deviation is not affected by adding or subtracting a constant.
Conclusion
Thus, the standard deviation of the variable (aX+b)/c is:
SD(aX+bc)=|a||c|σ
The correct answer is:
(c) |a/c|σ
We are transforming the variable X using the formula (aX+b)/c. This transformation involves multiplying X by a, adding b, and then dividing by c.
When we multiply a variable by a constant a, the standard deviation is also multiplied by the absolute value of that constant. Thus, the standard deviation of aX will be |a|σ.
Next, when we divide by c, the standard deviation is divided by the absolute value of c. Therefore, the standard deviation of (aX)/c will be |a|σ/|c|.
Now, we combine the effects of multiplying by a and dividing by c:
SD(aXc)=|a||c|⋅σ
Adding b to the variable does not affect the standard deviation. The standard deviation remains the same after adding or subtracting a constant.
Thus, the standard deviation of the variable (aX+b)/c is:
SD(aX+bc)=|a||c|σ
(c) |a/c|σ
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let x1,x2,x3,……..,xn be n observations with mean ¯x and standard deviation σ. The mean the standard deviation of kx1,kx2,……,kxn respectively are
(i) ¯x,kσ
(ii) k¯x,σ
(iii) k¯x,kσ
(iv) ¯x,σA¯x,kσBk¯x,σCk¯x,kσD¯x,σGiven r=√34,byx=12, variance of x=12, then standard deviation of y is
A2B3C4D9
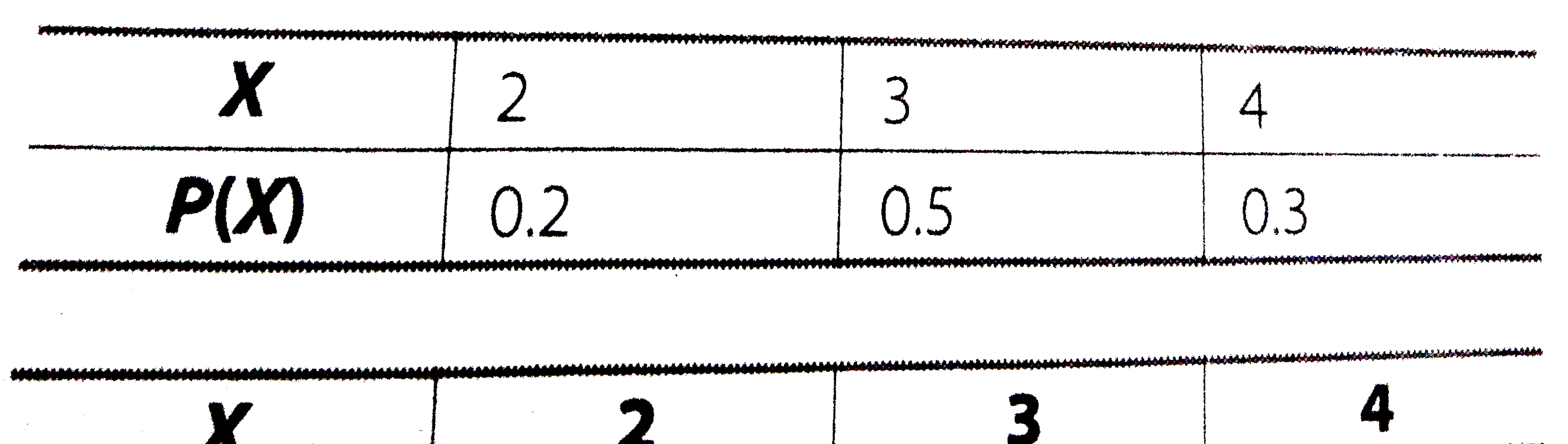
For the following probability distribution determine standard deviation of the random variable X.
View SolutionThe standard deviation of first 10 natural numbers is (a) 8.25 (b) 6.5 (c) 3.87 (d) 2.87
View SolutionThe standard deviation of first 10 natural numbers is (a) 8.25 (b) 6.5 (c) 3.87 (d) 2.87
View SolutionThe standard deviation of first 10 natural numbers is
a) 8.25
(b) 6.5
(c) 3.87
(d) 2.87
View SolutionLet a, b, c, d, e, be the observations with mean m and standard deviation s. The standard deviation of the observations a+k, b+k, c+k, d+k, e+k is (a) s (b) ks (c) s+k (d) sk
View SolutionLet x1,x2,,xn be xn observations. Let yi=axi+b for i=1,2,...,n where a and b are constants. If the mean of xi's is 48 and their standard deviation is 12, the mean of yi's is 55 and standard deviation of yi's is 15, the values of a and b are (a) a=1.25,b=−5 (b) a=−1.25,b=5 (c) a=2.5,b=−5 (d) a=2.5,b=5
View Solution