If the standard deviation of a variable X is σ , then standard deviation of variable aX+bc is (a) aσ (b) acσ (c) ∣∣ac∣∣σ (d) aσ+bc
To find the standard deviation of the variable (aX+b)/c given that the standard deviation of X is σ, we can follow these steps:
Step 1: Understand the transformation
We start with the variable X and we are transforming it into the new variable (aX+b)/c. Here, a, b, and c are constants.
Step 2: Identify the effect of constants on standard deviation
The standard deviation is affected by linear transformations. Specifically:
- If you multiply a variable by a constant a, the standard deviation is also multiplied by the absolute value of that constant, |a|.
- Adding a constant b does not affect the standard deviation.
Step 3: Apply the transformation
For the transformation (aX+b)/c:
- First, consider the multiplication by a. The standard deviation of aX is |a|σ.
- Next, dividing by c affects the standard deviation as well. The standard deviation of (aX)/c is |a|σ/|c|.
Step 4: Combine the effects
Thus, the standard deviation of (aX+b)/c can be expressed as:
Standard Deviation=|a||c|σ
Conclusion
Therefore, the standard deviation of the variable (aX+b)/c is |a/c|σ. The correct answer is (c) |a/c|σ.
We start with the variable X and we are transforming it into the new variable (aX+b)/c. Here, a, b, and c are constants.
The standard deviation is affected by linear transformations. Specifically:
- If you multiply a variable by a constant a, the standard deviation is also multiplied by the absolute value of that constant, |a|.
- Adding a constant b does not affect the standard deviation.
For the transformation (aX+b)/c:
- First, consider the multiplication by a. The standard deviation of aX is |a|σ.
- Next, dividing by c affects the standard deviation as well. The standard deviation of (aX)/c is |a|σ/|c|.
Thus, the standard deviation of (aX+b)/c can be expressed as:
Standard Deviation=|a||c|σ
Therefore, the standard deviation of the variable (aX+b)/c is |a/c|σ. The correct answer is (c) |a/c|σ.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let x1,x2,x3,……..,xn be n observations with mean ¯x and standard deviation σ. The mean the standard deviation of kx1,kx2,……,kxn respectively are
(i) ¯x,kσ
(ii) k¯x,σ
(iii) k¯x,kσ
(iv) ¯x,σA¯x,kσBk¯x,σCk¯x,kσD¯x,σGiven r=√34,byx=12, variance of x=12, then standard deviation of y is
A2B3C4D9
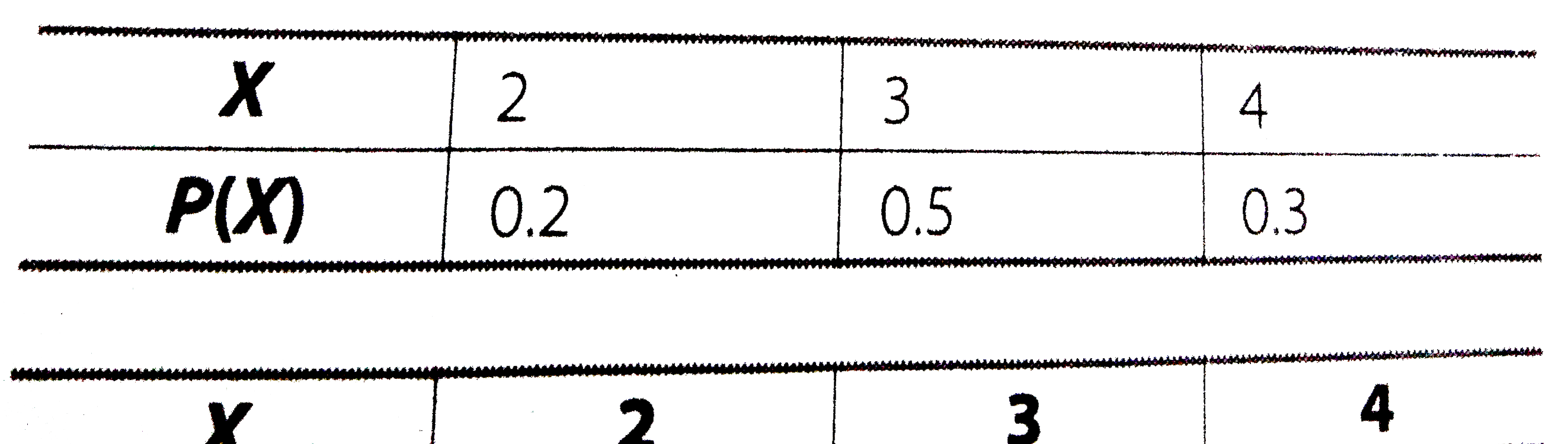
For the following probability distribution determine standard deviation of the random variable X.
View SolutionThe standard deviation of first 10 natural numbers is (a) 8.25 (b) 6.5 (c) 3.87 (d) 2.87
View SolutionThe standard deviation of first 10 natural numbers is (a) 8.25 (b) 6.5 (c) 3.87 (d) 2.87
View SolutionThe standard deviation of first 10 natural numbers is
a) 8.25
(b) 6.5
(c) 3.87
(d) 2.87
View SolutionLet a, b, c, d, e, be the observations with mean m and standard deviation s. The standard deviation of the observations a+k, b+k, c+k, d+k, e+k is (a) s (b) ks (c) s+k (d) sk
View SolutionLet x1,x2,,xn be xn observations. Let yi=axi+b for i=1,2,...,n where a and b are constants. If the mean of xi's is 48 and their standard deviation is 12, the mean of yi's is 55 and standard deviation of yi's is 15, the values of a and b are (a) a=1.25,b=−5 (b) a=−1.25,b=5 (c) a=2.5,b=−5 (d) a=2.5,b=5
View Solution
