Let Z be the set of integers. If A = {x∈Z:2(x+2)(x2−5x+6)=1 and B={x∈Z:−3<2x−1<9}, then the number of subsets of the set A × B is
218
210
215
212
The correct Answer is:C
To solve the problem, we need to find the sets A and B and then calculate the number of subsets of the Cartesian product A × B.
Step 1: Finding Set A
We start with the equation given for set A:
A={x∈Z:2(x+2)(x2−5x+6)=1}
The expression 2k=1 holds true if k=0. Therefore, we set the exponent equal to zero:
(x+2)(x2−5x+6)=0
Step 2: Factoring the Quadratic
Next, we need to factor the quadratic expression x2−5x+6:
x2−5x+6=(x−2)(x−3)
Step 3: Setting Up the Equation
Now we can rewrite the equation:
(x+2)(x−2)(x−3)=0
Step 4: Finding the Roots
Setting each factor to zero gives us the solutions:
1. x+2=0⇒x=−2
2. x−2=0⇒x=2
3. x−3=0⇒x=3
Thus, the set A is:
A={−2,2,3}
Step 5: Finding Set B
Now we move on to set B, which is defined as:
B={x∈Z:−3<2x−1<9}
Step 6: Solving the Inequality
We can break this into two inequalities:
1. 2x−1>−3
2. 2x−1<9
Solving the First Inequality
2x−1>−3⟹2x>−2⟹x>−1
Solving the Second Inequality
2x−1<9⟹2x<10⟹x<5
Step 7: Finding the Integer Solutions
Combining these results, we find:
−1<x<5⟹x∈{0,1,2,3,4}
Thus, the set B is:
B={0,1,2,3,4}
Step 8: Calculating the Cartesian Product A × B
The Cartesian product A×B consists of all ordered pairs (a,b) where a∈A and b∈B. The number of elements in A is 3 and in B is 5. Therefore, the number of elements in A×B is:
|A×B|=|A|×|B|=3×5=15
Step 9: Finding the Number of Subsets
The number of subsets of a set with n elements is given by 2n. Thus, the number of subsets of A×B is:
Number of subsets=215
Final Answer
The number of subsets of the set A×B is 215.
---
2. x−2=0⇒x=2
3. x−3=0⇒x=3
2. 2x−1<9
Topper's Solved these Questions
- JEE 2019BOOK - CENGAGE ENGLISHCHAPTER - JEE 2019EXERCISE - Chapter 1
5 Videos
- JEE 2019BOOK - CENGAGE ENGLISHCHAPTER - JEE 2019EXERCISE - Chapter 2
7 Videos
- JEE 2019BOOK - CENGAGE ENGLISHCHAPTER - JEE 2019EXERCISE - chapter -3
1 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Archives (Numerical Value type)
2 Videos
- LIMITSBOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - Comprehension Type
4 Videos
Similar Questions
Knowledge Check
If −5<2x−3≤x+2,x∈R, then the solution set of x on the number line is
A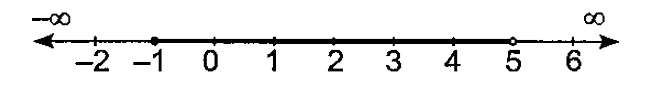 B
B C
C D
D
If 2x−3<x+1<4x+7,x∈R then the solution set of x on the number line is:
A B
B C
C D
D
If 2x−5≤5x+4<29 and x is an integer, then the solution set of x is
A{−2,−1,0,1,2,3,4,5}B{−2,−1,0,1,2,3,4}C{−3,−2,−1,0,1,2,3,4,5}D{−3,−2,−1,0,1,2,3,4}
Let Z denoted the set of integers, then
{x∈Z|x−3∣<4}∩{x∈Z|x−4∣<5}=
View SolutionLet A={x:xεz and 2(x+2)(x2−5x+6)=1},B={x:xεz and −3<2x−1<9}. Find number of subsets of cartesian product A×B (A) 218 (B) 210 (C) 215 (D) 220
View SolutionWrite the following sets in the roster form :
(i){x:x2−5x+6=0,x∈N} (ii){x:2x−5<4,x∈Z}
View SolutionThe number of intergal values of x if 5x−1<(x+1)2<7x−3 is
View SolutionIf A={x:x∈Nandx<614} and B={x:x∈Nandx2≤5) the number of subsets of set A×(A∩B) which contains exactly 3 elements is:
View Solution
