Let Z is be the set of integers , if A={x∈Z|x−3∣(x2−5x+6)=1}andB{x∈Z:10<3x+1<22}, then the number of subsets of the set A×B is
26
28
215
29
The correct Answer is:A
To solve the problem, we need to find the sets A and B and then determine the number of subsets of the Cartesian product A × B. Let's break it down step by step.
Step 1: Determine the Set A
We have the set defined as:
A={x∈Z:|x−3|(x2−5x+6)=1}
To analyze this, we can break it down into cases based on the properties of exponents and absolute values.
1. Case 1: |x−3|=1
- This gives us two equations:
- x−3=1 → x=4
- x−3=−1 → x=2
2. Case 2: x2−5x+6=0
- Factoring gives us:
(x−2)(x−3)=0
- This results in:
- x=2
- x=3 (but we will discard this since it leads to zero in the exponent)
Since |x−3|(x2−5x+6)=1 can also hold if the exponent is zero (which we already considered), we conclude that the valid integers for set A are:
A={2,4}
Step 2: Determine the Set B
The set B is defined as:
B={x∈Z:10<3x+1<22}
We can solve this compound inequality:
1. From 3x+1>10:
3x>9
x>3
2. From 3x+1<22:
3x<21
x<7
Combining these results, we find:
3<x<7
The integers satisfying this condition are:
B={4,5,6}
Step 3: Calculate the Number of Elements in A and B
- The number of elements in set A:
|A|=2
- The number of elements in set B:
|B|=3
Step 4: Calculate the Number of Elements in A × B
The number of elements in the Cartesian product A×B is given by:
|A×B|=|A|×|B|=2×3=6
Step 5: Calculate the Number of Subsets of A × B
The number of subsets of a set with n elements is given by 2n. Therefore, the number of subsets of A×B is:
Number of subsets=2|A×B|=26=64
Final Answer
The number of subsets of the set A×B is 64.
---
We have the set defined as:
A={x∈Z:|x−3|(x2−5x+6)=1}
- This gives us two equations:
- x−3=1 → x=4
- x−3=−1 → x=2
- Factoring gives us:
(x−2)(x−3)=0
- This results in:
- x=2
- x=3 (but we will discard this since it leads to zero in the exponent)
A={2,4}
The set B is defined as:
B={x∈Z:10<3x+1<22}
1. From 3x+1>10:
3x>9
x>3
3x<21
x<7
3<x<7
B={4,5,6}
- The number of elements in set A:
|A|=2
- The number of elements in set B:
|B|=3
The number of elements in the Cartesian product A×B is given by:
|A×B|=|A|×|B|=2×3=6
The number of subsets of a set with n elements is given by 2n. Therefore, the number of subsets of A×B is:
Number of subsets=2|A×B|=26=64
The number of subsets of the set A×B is 64.
Similar Questions
Knowledge Check
If 2x−3<x+1<4x+7,x∈R then the solution set of x on the number line is:
A B
B C
C D
D
If −1<3+4x≤23,x∈R (real numbers), then the solution set of x is
A−1≤x<5,x∈RB−1<x≤5,x∈RC−1≤x≤5,x∈RD−1<x<5,x∈RIf −5<2x−3≤x+2,x∈R, then the solution set of x on the number line is
A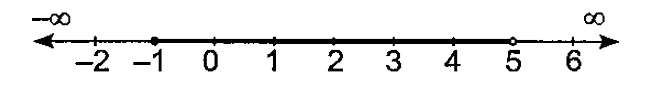 B
B C
C D
D
Let Z denoted the set of integers, then
{x∈Z|x−3∣<4}∩{x∈Z|x−4∣<5}=
View SolutionLet A={x:xεz and 2(x+2)(x2−5x+6)=1},B={x:xεz and −3<2x−1<9}. Find number of subsets of cartesian product A×B (A) 218 (B) 210 (C) 215 (D) 220
View SolutionLet P ={x:x is a positive integer ,x<6}
View SolutionIf A={x:x∈Nandx<614} and B={x:x∈Nandx2≤5) the number of subsets of set A×(A∩B) which contains exactly 3 elements is:
View SolutionIf 2x−5≤5x+4<29 and x is an integer, then the solution set of x is
View Solution