Suppose A, B are two points on 2x−y+3=0andP(1,2) is such that PA=PB. Then the mid point of AB is
(−15,135)
(−75,95)
(75,−95)
(−75,−95)
The correct Answer is:A
To solve the problem, we need to find the midpoint of points A and B on the line 2x−y+3=0 such that the distances from point P(1, 2) to points A and B are equal (i.e., PA=PB).
1. Identify the line equation and point P:
The line equation is given as 2x−y+3=0. We can rewrite this in slope-intercept form:
y=2x+3
The point P is given as P(1,2).
2. Use the distance formula:
Since PA=PB, point P lies on the perpendicular bisector of segment AB. Thus, we need to find the foot of the perpendicular from point P to the line 2x−y+3=0.
3. Find the coefficients for the line:
The line 2x−y+3=0 has coefficients:
- a=2
- b=−1
- c=3
4. Use the formula for the foot of the perpendicular:
The coordinates of the foot of the perpendicular from point P(x1,y1) to the line ax+by+c=0 can be calculated using:
(x,y)=(x1−a(ax1+by1+c)a2+b2,y1−b(ax1+by1+c)a2+b2)
Substituting P(1,2) into the formula:
x=1−2(2⋅1−1⋅2+3)22+(−1)2
y=2−−1(2⋅1−1⋅2+3)22+(−1)2
5. Calculate ax1+by1+c:
ax1+by1+c=2⋅1−1⋅2+3=2−2+3=3
6. Substituting into the foot of the perpendicular formula:
x=1−2⋅35=1−65=1−1.2=−0.2=−15
y=2−−1⋅35=2+35=2+0.6=2.6=135
7. Coordinates of the foot of the perpendicular:
The foot of the perpendicular P′ is at:
P′(−15,135)
8. Midpoint of AB:
Since P′ is the midpoint of segment AB, the coordinates of the midpoint of AB are:
Midpoint=P′(−15,135)
Final Answer:
The midpoint of points A and B is:
(−15,135)
The line equation is given as 2x−y+3=0. We can rewrite this in slope-intercept form:
y=2x+3
The point P is given as P(1,2).
Since PA=PB, point P lies on the perpendicular bisector of segment AB. Thus, we need to find the foot of the perpendicular from point P to the line 2x−y+3=0.
The line 2x−y+3=0 has coefficients:
- a=2
- b=−1
- c=3
The coordinates of the foot of the perpendicular from point P(x1,y1) to the line ax+by+c=0 can be calculated using:
(x,y)=(x1−a(ax1+by1+c)a2+b2,y1−b(ax1+by1+c)a2+b2)
Substituting P(1,2) into the formula:
x=1−2(2⋅1−1⋅2+3)22+(−1)2
y=2−−1(2⋅1−1⋅2+3)22+(−1)2
ax1+by1+c=2⋅1−1⋅2+3=2−2+3=3
x=1−2⋅35=1−65=1−1.2=−0.2=−15
y=2−−1⋅35=2+35=2+0.6=2.6=135
The foot of the perpendicular P′ is at:
P′(−15,135)
Since P′ is the midpoint of segment AB, the coordinates of the midpoint of AB are:
Midpoint=P′(−15,135)
The midpoint of points A and B is:
(−15,135)
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)
30 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)
27 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
A and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
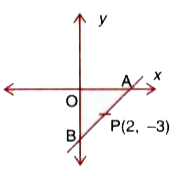
slope of line AB
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the

equation of line AB.
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the

co-ordinates of A and B.
View SolutionIf A and B are two fixed points and P is a variable point such that PA+PB=4, the locus of P is
View SolutionFind the eqution of the curve passing through the point (1,1), if the tangent drawn at any point P(x,y) on the curve meets the coordinate axes at A and B such that P is the mid point of AB.
View SolutionA straight line through the point (1,1) meets the X-axis at A and Y-axis at B. The locus of the mid-point of AB is
View SolutionA (c,0) and B (-c,0) are two points . If P is a point such that PA + PB = 2a where 0<c<a, then find the locus of P.
View SolutionA(−2,0)andB(2,0) are two fixed points and P 1s a point such that PA−PB=2 Let S be the circle x2+y2=r2 , then match the following. If r=2, then the number of points P satisfying PA−PB=2 and lying on x2+y2=r2 is
View SolutionPoints A and B have co-ordinates (3, 5) and (x, y) respectively. The mid-point of AB is (2, 3). Find the values of x and y.
View SolutionIf A(-3,4) ,B(5,6),then find point P on x-axis such that PA+PB is Minimum.
View Solution
